联系人:梁思涵/林志朋/刘富兵

一、包含转债个券赎回意愿差异的CCBA定价模型。
可转债在满足赎回条款后,发行人有权选择是否执行条款。当发行人赎回意愿强时,投资者预期转债的实际存续期较短,转债价格便会较低,可见赎回意愿在一定程度上会影响转债的价格。本文基于专题报告《可转债定价模型与应用》中的CCB模型以及转债赎回与不赎回的公告数据,通过对赎回保护期的概率分布进行建模,从而在转债定价中实现了对赎回意愿的刻画,形成了新的赎回概率调整定价模型CCBA(Callable Convertible Bond Adjusted)。该CCBA模型相对于传统的CCB模型与蒙特卡洛模拟模型有着如下的优势与提升:
① 相对于CCB模型。由于加入了赎回意愿的变化,CCBA模型在相对定价与绝对定价两个维度均有一定的提升。1)相对定价:CCB定价模型中没有体现出个券赎回意愿的差异,其假设所有转债的赎回意愿均较强,因此CCB选债策略易选出赎回意愿强的转债,如金融转债。而加入个券赎回意愿差异的CCBA模型,相当于对赎回意愿进行了“中性化”,使得选债策略超额收益更加稳定。2)绝对定价:最近几年整体转债市场估值提升的原因之一为赎回意愿的弱化,赎回意愿的弱化使得转债期望存续期更长,理论定价应当更高。因此我们将赎回意愿变化考虑在定价之后,得到的市场CCBA定价偏离度中枢更加稳定且接近于0,对择时有相对更好的效果。
② 相对于蒙特卡洛模拟模型。蒙特卡洛模拟为常用来刻画赎回意愿的定价模型,然而该模型的核心应该是在于如何建模赎回意愿,而非蒙特卡洛模拟本身。因此当我们调整赎回意愿模型时需要经常批量重新模拟路径并计算新定价,该过程较为耗时。而CCBA模型是基于CCB模型构建,CCB模型本身是解析解运算效率高,因此我们可以专注于对赎回意愿进行建模,使得定价模型的效率与效果皆优。
二、对于CCBA定价模型,本文主要有以下两点应用:
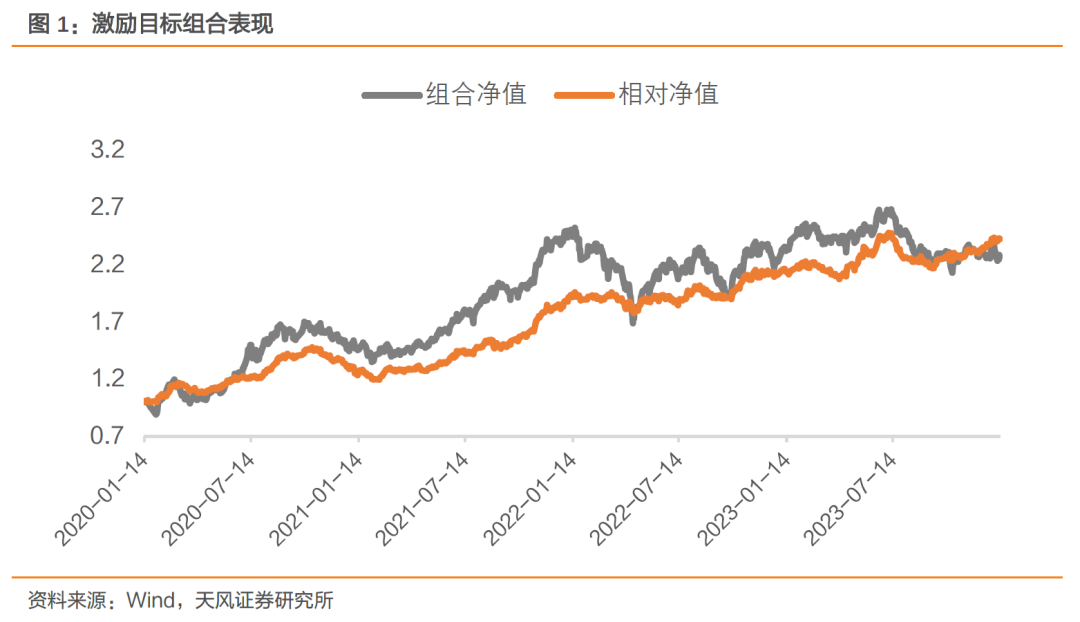
① 平衡转债增强策略。我们构建了CCBA定价偏离因子=转债真实价格/CCBA模型定价-1,该因子在平衡转债中能够实现稳定的超额收益。基于CCBA定价偏离因子构建的平衡转债增强策略,从2020年开始相对于平衡基准能够实现年化10.6%的超额收益,信息比率2.60,在2023年也能实现15.1%的绝对收益,同时波动与回撤分别仅有8.8%与5.3%。
② 择时策略。我们基于信用债与转债YTM之差和市场CCBA定价偏离度可以实现对转债&国债的择时策略,当信用债与转债YTM之差较低且CCBA估值较低时,说明转债市场已经处于估值低位,且相对于股票的敏感性已经较低,此时下行空间有限,择时策略便会超配转债资产,该策略从2008年开始能够实现9.26%的年化收益,显著优于2.99%的策略基准。
可转债的赎回条款是对可转债价格影响最大的条款,近几年转债的赎回意愿出现较大的变化,对应也会影响转债的定价与估值。当转债赎回意愿较强时,投资者预计其手中的转债在两年左右大概率便被赎回,相当于转债是一个两年左右的看涨期权。而当转债的赎回意愿较弱时,投资者便预期转债可能是一个三至四年才会被赎回结束的期权,其市场定价便会上升。由此可见,赎回意愿对于转债价格影响显著,有着一定的研究价值。因此在引言部分我们尝试讨论以下三个问题:• 赎回意愿在转债绝对定价中的意义是什么?
• 哪种定价模型可以体现出转债赎回意愿的变化?
① 赎回意愿在转债相对定价中的意义。转债相对定价即通过截面中转债估值因子的高低进行排序,主要目的在于选择估值相对较低的转债,从而实现稳定的超额收益。对于市场预期赎回意愿强的转债,如金融类转债(历史上满足赎回条件后极大概率赎回),其市场定价便会相对较低。因此将赎回意愿加入定价中的意义如下所示(其中后文数据均截止至2024年2月2日):• 传统模型易选出市场预期赎回意愿强的转债:传统的转债定价模型中没有体现出个券赎回意愿的差异,如上一篇转债定价专题报告《可转债定价模型与应用》中的CCB定价偏离因子便是假设所有转债赎回意愿均较强,因此赎回意愿较强的转债(如金融转债)的估值便会显得较低。如图表1中我们在平衡转债中通过CCB定价偏离因子选择低估转债时,发现策略持有的金融类转债占比要远高于市场平均。• 将赎回意愿加入转债定价相当于对赎回意愿进行了“中性化”:超配赎回意愿强的转债并不一定能够产生稳定的超额收益,因此我们通过在转债定价中加入个券赎回意愿的差异,可以对赎回意愿较强的转债给出较低的定价,反之对于赎回意愿较弱的转债给出较高的定价。从而使得低估值策略对赎回意愿进行了“中性化”,实现了更稳定的超额收益。

② 赎回意愿在转债绝对定价中的意义。绝对定价即通过衡量真实价格与模型定价的绝对差距来判断转债的估值水平,而并非截面排序。绝对定价的主要目的在于衡量整体市场估值水平与择时、可转债套利策略等。首先我们可以使用常见的百元溢价率指标展现市场估值,我们通过转股溢价率与平价进行反比例回归,样本权重为个券转债市值,并取平价为100时的转股溢价率作为百元溢价率指标。由下图可以看出,转债市场的溢价率水平自从2019年以来便开始逐渐走高,一直到2022年初之后才开始围绕着新的中枢震荡。
转债市场估值上行的原因主要有两点:1)最近几年以“固收+”为收益目标的资金增加,对转债需求量加大,从而使得转债估值出现被动抬升,然而资金需求对转债估值的影响较难通过定量的方式进行刻画。2)另一部分原因为转债发行人的赎回意愿降低,从而使得转债的估值抬升,赎回意愿对定价的影响更容易通过定量的方式刻画。我们统计了每半年内满足赎回条件的转债个数与其中选择执行赎回条款的转债个数,并计算了两者之间的比值称为赎回比例。由下图可以看出,赎回比例自2020年便开始逐渐降低,代表了发行人赎回意愿的弱化。此时投资者便会预期转债的实际存续时间较前几年更长,市场定价便会更高。由此可见,研究赎回意愿对于转债的绝对定价也是有一定意义的。

③ CCB定价模型适合刻画转债的赎回意愿。目前常用的刻画赎回意愿的定价方式是蒙特卡洛模拟,即假设一个赎回概率P,当模拟的平价路径碰到赎回线后便会以P为概率赎回。然而基于赎回概率的定价模型的核心是在于如何建模赎回概率P,而非蒙特卡洛模拟本身。因此当我们在建模P时需要经常批量重新模拟路径并计算新定价,该过程较为耗时。因此本文在前述专题报告《可转债定价模型与应用》中CCB定价模型的基础上,通过较为科学高效的方式对赎回意愿进行了建模与定价。此处我们可以先回顾一下CCB模型的特性,该模型假设转债存在赎回保护期tp。在tp之前若转债满足赎回条件,则转债不会选择执行赎回条款。而在tp之后若转债满足了赎回条件,则转债会选择执行赎回条款。该模型的优点为可以仅通过调整赎回保护期参数来体现出转债发行人赎回意愿的强弱:若输入的赎回保护期较长(短),则体现出发行人赎回意愿较弱(强),模型定价也会较高(低)。其中图表4中h代表平价赎回线,S_0代表当前平价,tp代表赎回保护期,tm代表剩余期限,fv_N代表到期时支付的转债面值与票息的终值。

因此本篇目的在于将市场赎回意愿引入到转债CCB定价模型中,从而得到更加贴近于真实市场情况的“可转债的赎回概率调整定价模型”,该模型在相对定价与绝对定价领域均有较好的应用效果。本篇主要引出并回答以下几个问题:• 赎回意愿的变化如何影响可转债定价?
• 引入赎回意愿后的定价模型有何优势,以及有什么应用?
2.1符号与变量的释义说明
此处我们对后文出现的符号与变量的释义进行说明:
• 转债存续期(D):代表转债相对于发行日已经存续的时间长度,单位为年。
• 赎回保护期(T_D):代表当转债位于存续期第D年时,赎回保护期长度为T_D,单位为年。转债在存续期为D+T_D年之前满足赎回条件后不会执行赎回条款,而在存续期为D+T_D年之后满足赎回条件后必会执行赎回条款。T_D的取值区间为0≤T_D≤转债剩余期限。示例如下图所示。
• 赎回保护期概率(P(T_D=n)):代表当转债位于存续期第D年时,赎回保护期T_D为n年的概率。• 赎回保护期下的CCB定价(CCB(T_D=n)):代表当转债位于存续期第D年,且赎回保护期T_D为n年时的CCB定价。

2.2赎回保护期的概率分布
• 进入转股期之前的赎回保护期:对于刚刚发行与上市的转债来说,在进入转股期之前是不允许被赎回的。一般从转债发行日到转股期开始日的时间长度在半年到三个季度左右,在这段时间内若转债满足了赎回条件,转债是不允许被赎回的。• 发出不赎回公告时的赎回保护期:若转债已经进入转股期,并且在某个时点满足了赎回条件,当转债发行人此时不想赎回转债时,便会发一个不赎回公告,并且说明未来一段时间不会执行赎回条款,这个时间长度一般在一个季度到半年左右。
上述提及的赎回保护期都是确定已知的,在该赎回保护期内的转债肯定不会被赎回。然而转债定价体现的是市场预期,即若一个转债尚未满足赎回条件或还没有进入转股期,但是市场普遍认为其即使满足赎回条件后也大概率不赎回的话,该转债的市场定价便会较高,因此我们需要建模并计算转债赎回保护期长度的期望值。
为了简单起见,我们首先可以讨论对于刚发行转债的赎回保护期T_(D=0)如何建模。原先我们对T_(D=0)的取值为从发行日到转股期开始日的时间长度,但实际上仅有赎回意愿很强的转债(如银行)的赎回保护期才有这么短,而有一些转债赎回意愿较弱,其赎回保护期应该就会较长。因此转债的赎回保护期其实应该是一个概率分布,假设我们利用历史数据统计得到类似下图的概率分布,我们便可以通过赎回保护期的概率对不同赎回保护期下的CCB定价进行加权求和,从而得到赎回概率调整后的CCB定价,简称为CCBA(Callable Convertible Bond Adjusted),CCBA定价的公式如下。下图为对于刚上市转债赎回保护期T_(D=0)概率分布与定价示例图。
由上可见,CCBA定价的关键点在于如何得到赎回保护期的概率分布。我们首先可以按照如下流程生成刚上市转债的赎回保护期T_(D=0)的概率分布,然后对于已经存续一段时间的转债,再基于T_(D=0)的概率分布进行调整,得到不同存续期m下的赎回保护期T_(D=m)的概率分布,并用概率加权CCB定价从而得到CCBA定价,具体步骤细节可见后文:
• 基于公告数据生成赎回与不赎回样本:我们统计了过去一段时间内,若转债满足赎回条件下,转债是否执行赎回条款的公告数据,通过该公告可判断转债赎回保护期的区间,并将区间数据处理生成赎回与不赎回的样本点数据。
• 通过Logistic回归得到赎回概率:我们将转债的赎回与不赎回样本作为被解释变量Y,X为转债存续期等可能会影响发行人赎回意愿的指标,并进行Logistic回归。即可生成转债的赎回概率期限结构。
• 生成赎回保护期的概率分布:赎回概率期限结构可以理解为对于刚上市转债的赎回保护期T_(D=0)的累计概率函数,我们将其以季度为间隔计算差分,便可得到T_(D=0)的概率分布。
• 计算赎回调整后的转债定价CCBA:基于刚上市转债的赎回保护期T_(D=0)的概率分布,我们可以根据个券已经发布的不赎回公告、存续期m等参数进行调整,得到个券赎回保护期T_(D=m)的概率分布,并对不同赎回保护期下的CCB定价计算加权求和得到CCBA定价。
2.3赎回与不赎回的样本生成
① 赎回与不赎回公告。当转债在满足赎回条件时,往往会在当天收盘后发出赎回或者不赎回公告。那么在公告发出后,我们可以得到以下三个关键日期:• 不赎回结束日:仅不赎回公告会有该日期,代表在该日期之前,转债满足条件也不会赎回,且在不赎回结束日之后会重新开始记录平价满足赎回线的日数。在2022年前很多转债在发布不赎回公告时未披露不赎回结束日,此时我们默认未来一个季度不赎回。
实际上,我们在采集转债赎回与不赎回公告相关样本时,很难基于公告数据直接得知转债的赎回保护期T_(D=0)是否为第n年,往往得到的都是赎回保护期T_(D=0)位于某个区间的样本,我们以两个真实的转债进行示例:• 若转债在存续期第n年满足条件后不赎回:如图表9转债示例A中,转债在2023/7/24满足赎回条件后选择未来3个月(至2023/10/24)不赎回转债,此时我们无法确定3个月之后发行人是否选择继续不赎回转债,因此我们只能确定其赎回保护期T_(D=0)至少为1.51年(2023/10/24距离转债发行日的时间长度)。而在之后的2023/11/24,转债发行人继续选择不赎回,赎回保护期下限被向上更新。因此,不赎回公告只能确定赎回保护期T_(D=0)>n年;• 若转债在存续期第n年满足条件并赎回:如图表10转债示例B中,转债在2021/12/16满足赎回条件后选择赎回转债,由于之前其并未满足过赎回条件来“说明”其是否赎回,因此我们只能确定其赎回保护期T_(D=0)最多为1.28年(2021/12/16距离转债发行日的时间长度)。因此,赎回公告只能确定赎回保护期T_(D=0)<n年;• 若转债在存续期第n年发出不赎回公告,在存续期第m年发出赎回公告:某些转债会同时发布过赎回与不赎回公告,此时可将前文两点结合,即可以确定赎回保护期T_(D=0)在[n,m]之间。

由于转债赎回相关公告披露的管理法规在近几年才趋于完善,因此之前几年转债在满足赎回条件后经常不披露执行或者不执行赎回条款的公告,具体数量可见图表11。因此,对于已经满足条件但是不发公告的情况,本文也默认为公告不赎回。例如,假设某转债在2021/1/1满足赎回条件但未发布公告,我们规定若其在两周后的2021/1/15仍未发布公告,则默认其不赎回,且令公告发布日为2021/1/15。

② 生成赎回与不赎回样本。基于上述公告数据我们仅可以得到赎回保护期T_(D=0)的区间,然而区间数据难以使用,我们需要将其转换成样本点。其中通过赎回与不赎回公告生成的样本点分别为:• 若转债在其存续期的第n年发出不赎回公告:此时可以判断转债的赎回保护期T_(D=0)肯定大于n年,即若在存续期n年之前的某个时间点满足赎回条件后转债也会选择不赎回。因此我们可以按照存续期季度为间隔,从转股期开始日到不赎回公告发布日生成“不赎回样本”。• 若转债在其存续期的第n年发出赎回公告:此时可以判断转债的赎回保护期T_(D=0)肯定小于n年,即若在存续期n年之后的某个时间点满足赎回条件后也会选择赎回。因此我们可以按照存续期季度为间隔,从满足赎回条件日到当前时点生成“赎回样本”。
由此可见,我们在得到赎回与不赎回公告之后,便可以按照季度为间隔生成赎回与不赎回样本,其中样本的获得日期取为该公告的发布日。按照季度为间隔生成样本的原因在于:一般发出不赎回公告时,最常用的不赎回期限为一个季度。
2.4基于Logistic回归得到赎回概率
① 赎回概率。下图为站在某个时点回看过去6年内发行的转债所产生的样本数量,我们以季度为间隔,按照样本的存续期进行分组形成柱状图。我们同样计算了每个季度赎回样本数与总样本数之间的比值,并称为“赎回概率”。赎回概率指的是当转债在存续期第n年满足赎回条件后执行赎回条款的概率,同样也代表着转债赎回保护期T_(D=0)小于n年的概率。然而通过比值计算的赎回概率会有以下两个缺点:• 数据质量不同:转债所提供的样本大多对应的存续期较短,很少有转债能够提供存续期较长的样本。因此当存续期较短时,赎回概率曲线的质量较高。而当存续期较长时,赎回概率曲线的数据质量较差。• 样本时效性不同:有些样本是基于几年前发布的公告所生成,而有些样本是基于最近发布的公告所生成,因此后者的时效性肯定要强于前者,理应赋予更高的权重。
可见直接使用比值的方式计算赎回概率效果较差,因此我们在下文使用了Logistic回归的方式来计算赎回概率。
② 基于Logistic回归得到赎回概率。为了能够更好的计算出转债的赎回概率,我们使用了Logistic回归模型。该模型的构建细节如下:• 被解释变量:若样本为“赎回样本”,则Y=1,若样本为“不赎回样本”,则Y=0;• 解释变量:样本所对应的转债存续期长度,单位为年;• 样本池:过去六年内发行的转债,发行规模三个亿以上,评级AA-及以上,非银行转债,从2018年开始每日滚动历史窗口;• 样本权重:按照样本的获得日期距离当前日期生成半衰期为一年的指数衰减权重。其中,样本的获得日期为生成样本时对应的赎回或不赎回公告的发布日。
我们每天滚动进行Logistic回归,从而生成转债存续期与赎回概率的曲线,我们可以称之为“转债赎回概率期限结构”。由图表13与14可见,2018-2019年转债赎回期限结构较陡峭,即转债在存续1~2年后若满足赎回条件便大概率执行赎回条款。而自从2020年年中开始至2024年2月初,赎回概率期限结构走平,即说明当前转债发行人的赎回意愿从2020年下半年开始便已经降低,该现象也较为符合前文图表3。

2.5其他影响赎回期限结构的变量
图表15与16展示的是Logistic模型的回归参数与R方,可以看出存续期对赎回概率的解释度在2019-2020年期间达到了最高,随后由于赎回意愿降低,模型解释度快速下降,当前R方在10.2%左右,因此我们可以尝试加入一些其他解释变量提升模型解释度。
那么什么样的变量是适合作为其他解释变量呢?我们在找其他解释变量时,往往会遇到以下两种。第一种为会随着时间发生改变的变量,其中符合逻辑的变量如正股公司大股东持有转债的占比、公司当前货币资金量、公司当前财务杠杆、权益市场当前处于上行或下行状态等。由于我们的目标是对转债未来6年的赎回概率进行测算,因此若解释变量是时变的,那我们需要先对解释变量的未来走势做出预期,才能基于该预期得到赎回概率期限结构,这是非常困难的,因此时变的变量不适合作为解释变量。
第二种为不随时间发生改变的变量,该类变量由于非时变,因此不需要对其进行预期,适合作为解释变量。我们按照逻辑,找到了以下几个可能有效的解释变量:• 转债大类行业:由于转债本身不同行业的特性,其赎回行为会受到行业的影响。由于转债数量较少且行业分布较散,因此我们以中信风格指数的方式将行业分为金融、周期、消费、成长、稳定这五类,并且在回归时将其作为0和1的变量。• 转债评级:评级在一定程度上代表了其还款的能力与意愿,因此也会影响转债的赎回意愿。在回归时我们将AAA-及以上作为高评级,将AA+及以下作为中评级,划分为0和1的变量。• 转债发行规模:发行规模代表了发行人在赎回或者兑付转债面值时候所面临的资金压力,对赎回行为会有一定影响。在回归时我们将10亿以下作为低规模,10至20亿作为中规模,20亿以上作为高规模,划分为0和1的变量。
各变量回归后的解释度R方如下图所示,可见变量在2019-2020年均有一定解释度。然而从2022年开始各变量的解释度均趋近于0,可见若直接将其带入回归模型中效果并不理想。其中可能的原因为,上述变量本身直接提供的解释度并不高,然而可能会影响转债的赎回概率期限结构。因此,我们尝试按照上述的行业、评级、发行规模这三个特征分别划分转债池,并在不同转债池子中仍使用存续期作为解释变量进行回归。

① 转债行业。我们分别在周期、消费、成长、稳定类行业转债中进行回归,其中金融由于仅有苏租转债有不赎回记录,赎回概率极高,此处不予展示。由下图可见,不同大类行业中存续期的解释度与赎回意愿有较为显著的差别。其中稳定性行业中由于公共电力行业转债经常选择不执行赎回条款,该大类行业当前的赎回意愿最低。
② 转债评级。我们分别在高评级(AAA-及以上)与中评级(AA+、AA、AA-)转债池中进行回归,由下图可见,高评级转债整体的赎回意愿较高,其赎回概率要远高于中评级转债。
③ 转债发行规模。我们分别在低规模(3至10亿)、中规模(10亿至20亿)、高规模(20亿及以上)转债池中进行回归,由下图可见,高规模与低规模转债的赎回意愿均高于中规模转债。
④ 结合多个特征。不同转债会具有不同的行业、评级与发行规模,那么我们如何将转债的这些不同特征融合在一起呢?此处我们的方法为,将这三个特征分别生成的赎回期限结构与市场赎回期限结构计算等权平均,形成对于该个券独有的赎回期限结构。例如,若一只转债属于周期行业、高评级、低发行规模特征,那我们可以分别将周期行业、高评级、低发行规模、全市场回归出来的四个赎回期限结构等权平均,形成对于该个券的赎回期限结构。
2.6由赎回概率到赎回保护期分布
基于前述模型,我们每天都可以得到针对于不同个券的赎回概率期限结构曲线。由前文的介绍可知,赎回概率期限结构上面的点代表的含义是,当转债在存续期第n年满足赎回条件后执行赎回条款的概率,同样也代表着转债赎回保护期T_(D=0)小于n年的概率。因此,赎回概率期限结构曲线其实就是赎回保护期T_(D=0)的累积概率分布函数,我们对其计算季频差分,便可以得到赎回保护期T_(D=0)分布。其中在计算赎回保护期T_(D=0)分布之前,需要对赎回期限结构进行以下三点调整:• 转债一般在发行半年到三个季度后才进入转股期,发行人在转股期开始后才允许执行赎回条款。因此对于每个个券,我们可以将转股期开始之前的赎回概率设置为0。• 由于转债最多6年便会到期,到期时转债必会按照面值+票息为赎回价进行赎回,因此我们可以将第6年(若是5年到期的转债则为第5年)的赎回概率设置为100%。• 对于银行类转债来说,其发转债的目的主要是为了等转债转股后补充一级资本金,赎回意愿非常强,因此我们令银行类转债的赎回概率在进入转股期后均为100%。
2.7计算赎回调整后的转债定价CCBA
前文我们所得到的是针对于刚上市转债赎回保护期T_(D=0)的概率分布建模,那么对于已经存续m年的转债来说,应如何得到其使用的赎回保护期T_(D=m)的概率分布呢?我们按照转债不同的已经存续的年数,以及是否发过赎回公告,可以将所有情况分为以下四种:
① 情况一:仍处于转股期之前的转债。以图表26中的转债为例,若此时转债刚刚存续m=0.25年,由于转债在转股期之前因此无赎回相关的公告数据,可直接使用刚上市转债的赎回保护期T_(D=0)的概率分布进行计算。我们按照如下步骤计算这种情况下的赎回调整定价CCBA:• 调整赎回保护期长度:将未来每个季度的存续期长度减去当前已经存续的时长作为赎回保护期T_(D=m)的不同取值。• 计算定价:计算不同赎回保护期T_(D=m)取值下的CCB定价,最后按照T_(D=m)的赎回概率分布对CCB定价加权求和得到CCBA定价。因此在情况一中,定价公式如下所示(其中在此示例中m=0.25):

② 情况二:处于转股期但没有发布过不赎回公告。以图表27中的转债为例,此时转债已存续m=1年,且已进入转股期,但尚未满足赎回条件,因此我们仍没有关于该个券赎回保护期的任何新信息。可以按照如下步骤计算赎回调整定价CCBA:• 调整赎回保护期长度:将未来每个季度的存续期长度减去当前已经存续的时长作为赎回保护期T_(D=m)的不同取值。• 调整赎回保护期概率分布:由于转债没有在存续期第m年之前发出过不赎回公告,因此赎回保护期T_(D=0)小于m年的概率P(T_(D=0)<m)仍然是存在的,不可去除。在情况二中,我们可以得到赎回保护期T_(D=m)的概率分布P(T_(D=m)=n)(其中在此示例中m=1):• 计算定价:计算不同赎回保护期T_(D=m)取值下的CCB定价,最后按照T_(D=m)的赎回概率分布对CCB定价加权求和得到CCBA定价。因此在情况二中,定价公式如下所示(其中在此示例中m=1):
为了方便理解第二种情况,我们可以举一个例子。例如有一只银行转债,基于上文我们可知其赎回意愿非常强。假设该转债发行日距离转股期开始日为0.5年,那么该刚发行的银行转债的赎回保护期概率分布为P(T_(D=0)=0.5)=100%。若该转债在存续期为2年时仍未满足赎回条件,我们仍然知道其一旦满足赎回条件必定会赎回。因此我们可以计算此时的赎回保护期概率分布为P(T_(D=2)=0)=P(T_(D=0)≤2)=100%,即代表了转债当前一旦满足赎回条件必定赎回。

③ 情况三:曾经发布过不赎回公告,且当前已经脱离公告不赎回区间。以图表28中的转债为例,此时转债已存续m1=1.5年,并且之前发出过不赎回公告,该公告宣告不赎回区间在存续期为m2=1年时结束,可见m1≥m2。此时我们可以确定该转债的赎回保护期T_(D=0)肯定大于m2年,因此可以按照如下步骤计算赎回调整定价:• 调整赎回保护期长度:将未来每个季度的存续期长度减去当前已经存续的时长作为赎回保护期T_(D=m1)的不同取值。• 调整赎回保护期概率分布:由于转债曾发布公告说明在存续期第m2年之前均不赎回,因此此时我们可以去除赎回保护期T_(D=0)小于m2年的概率,即令P(T_(D=0)<m2)=0。然而在存续期第m2年与第m1年之间并没有说明不赎回,因此P(m2≤T_(D=0)≤m1)仍然是存在的。由于我们去除了P(T_(D=0)<m2)的概率,所以在最后计算P(T_(D=m1)=n)时需要将概率归一化到100%。因此在情况三中,我们可以得到赎回保护期T_(D=m1)的概率分布P(T_(D=m1)=n)(其中在此示例中m1=1.5,m2=1):• 计算定价:计算不同赎回保护期T_(D=m1)取值下的CCB定价,最后按照T_(D=m1)的赎回概率分布对CCB定价加权求和得到CCBA定价。因此在情况三中,定价公式如下所示(其中在此示例中m1=1.5):

④ 情况四:发布过不赎回公告,当前仍处于不赎回期。以图表29中的转债为例,此时转债已存续m1=1.5年,最近刚发了不赎回公告,并且该公告宣告不赎回区间在存续期为m2=2年时结束,可见m1<m2,所以当前仍然处于不赎回区间。此时我们可以确定该转债的赎回保护期T_(D=0)肯定大于m2年,因此可以按照如下步骤计算赎回调整定价:• 调整赎回保护期长度:将未来每个季度的存续期长度减去当前已经存续的时长作为赎回保护期T_(D=m1)的不同取值。• 调整赎回保护期概率分布:由于转债发布公告说明在存续期第m2年之前均不赎回,因此此时我们可以去除赎回保护期T_(D=0)小于m2年的概率,即令P(T_(D=0)<m2)=0。由于我们去除了P(T_(D=0)<m2)的概率,所以在最后计算P(T_(D=m1)=n)时需要将概率归一化到100%。因此在情况四中,我们可以得到赎回保护期T_(D=m1)的概率分布P(T_(D=m1)=n)(其中在此示例中m1=1.5,m2=2):• 计算定价:计算不同赎回保护期T_(D=m1)取值下的CCB定价,最后按照T_(D=m1)的赎回概率分布对CCB定价加权求和得到CCBA定价。因此在情况四中,定价公式如下所示(其中在此示例中m1=1.5):
2.8CCBA定价结果展示
我们以下图的真实转债作为示例,展示赎回调整后定价的CCBA模型与之前没有做过赎回调整的CCB模型之间的差别。由下图可见,该转债从上市以来便属于偏股转债,之前的CCB模型假设转债赎回意愿很强,因此定价较低且紧贴于平价。而经过赎回概率调整后的CCBA模型将转债赎回意愿的下降体现在了定价之中,使得模型定价相对于平价有一定的溢价,定价与真实价格更加接近。

我们使用BS模型、CCB模型、CCBA模型分别对所有转债进行定价,同时计算定价偏离度(真实价格/模型定价-1),以及平均定价误差(定价偏离度绝对值的平均值)。CCB定价偏离度是假设赎回意愿很强时转债市场的估值水平,BS定价偏离度是假设转债永远不提前赎回时市场的估值水平,而CCBA定价偏离度是动态反应出发行人赎回意愿的情况下市场的估值水平。由图表31可见,在2020年之前转债赎回意愿较强,CCBA模型贴近于CCB模型。而由于赎回意愿的下降,CCBA模型在2020年之后开始逐渐贴近于BS模型。由图表32可见,在三种定价方法中,平均来看CCBA定价偏离度的历史中位数稳定性更高,是个中枢相对更稳定的估值方法。
2.9可转债价格隐含的其他信息
那么转债价格中隐含着哪些信息呢?首先我们可以计算真实的赎回保护期与转债价格隐含的赎回保护期,并对两者进行比较。由此我们计算了以下两个指标:
• 市场平均赎回保护期:我们对前文统计的赎回保护期概率分布计算期望值E(T_(D=0)),代表统计出来的真实市场平均赎回保护期。• 价格隐含赎回保护期:我们基于CCB模型,将赎回保护期设置为未知数,通过真实价格倒推出隐含的赎回保护期,并取刚刚发行半年内的转债的隐含赎回保护期计算等权平均。
由下图可以看出,当前统计的市场平均赎回保护期为2.8年左右,说明转债在存续期2.8年内满足赎回条件后大概率会选择不执行赎回条款。对于刚发行的转债,当前其价格隐含的赎回保护期为2.9年,已较为接近实际统计的2.8年。然而在2022年初至2023年底期间,隐含赎回保护期经常显著高于统计的市场平均赎回保护期,说明转债价格还体现了对其他因素的预期。
那么转债价格还体现了什么信息?我们可以将转债比作一个基于转债平价的期货,若投资者对该“期货”需求量很大或看涨情绪很强,则该“期货”可能会相对于现货出现大幅的升水,即转债真实价格相对于模型产生显著溢价,如2021年下半年至2023年底的转债市场便是类似这种情况。为了体现出这个现象,我们可以将CCBA模型中的平价设置为未知数,并基于转债真实价格倒退出“隐含平价”,同时计算“透支平价涨跌幅”=隐含平价/当前真实平价-1。由下图可见:• 平衡与偏债转债对平价的透支幅度高于偏股:当前偏债、平衡、偏股的透支平价涨跌幅分别为-4.8%、-2.2%、-5.1%,而在2022年初至2023年底期间,平衡与偏债转债的透支平价涨跌幅要远高于偏股转债。其中一部分原因在于平衡与偏债转债未来有较大概率执行下修条款,因此对平价的透支中隐含了一部分的下修预期。• 转债对平价的透支幅度与平价历史涨跌幅有关:若转债投资者对未来权益市场有着预期能力,则透支平价涨跌幅应和未来真实平价涨跌幅有关。但实际上正好相反,由图表35可以看出,透支平价涨跌幅与过去一个季度平价涨跌幅相关。即若过去一段时间平价涨幅较高,则转债价格中便会隐含一定的动量效应,转债估值易透支平价的涨幅,使得转债估值较高,如2022年初。

3.1转债CCBA定价偏离因子选债策略
① 平衡转债增强策略。首先我们可以构建CCBA定价偏离因子=转债真实价格/CCBA模型定价-1来进行相对选债,当因子越低时说明该转债越被低估。我们沿用《可转债定价模型与应用》中的回测框架,细节如下:• 回测时间:2018年1月到2024年2月,双周度调仓。• 转债限制:1)转债余额大于等于3亿元;2)转债外部评级AA-及以上;3)开仓时转债非全天停牌,尚未发出赎回公告,正股非ST,以及距离转债到期日大于三个月。
• 回测方法:每双周计算个券的平底溢价率(平价/债底-1),并按照±15%分为偏债、平衡与偏股这三个分域,在这三个分域中各自选择估值最低的不超过30只转债进行配置。
我们按照上述框架分别在偏债、平衡、偏股中对CCB与CCBA定价偏离因子进行了回测,下图为从2020年开始两个因子在三个分域中的年化超额收益,基准为满足转债限制的对应偏债、平衡、偏股的等权指数。可以看出,在偏债与偏股中,CCBA因子相对于CCB因子并没有显著优势,主要原因在于:• 偏股转债:我们曾在报告《可转债估值因子的衰退与优化思路》中讨论过,由于偏股转债本身接近于股票,其估值高低基本仅受到市场对正股未来表现的预期,以及对是否赎回的预期。最近几年正股博弈与赎回博弈的有效性均显著提高,即使加入赎回意愿的调整,也已很难通过低估值类因子获得稳定的超额收益。• 偏债转债:偏债转债本身受到赎回条款的影响较小,因此CCB与CCBA因子的差距较为有限。

尽管在偏债与偏股转债中CCBA因子相对于CCB因子没有显著优势,但在平衡转债中,CCBA因子要显著优于CCB因子。从2020年开始,在平衡转债中CCBA因子每年的超额收益均能保持在10%左右的水平,同时信息比率能够达到2.60。在2023年也能实现15.1%的绝对收益,同时波动与回撤分别仅有8.8%与5.3%。
那么为何CCBA因子能够在平衡转债中实现显著且稳定的超额收益呢?我们认为主要有以下两点原因:• 期权属性在平衡转债中最为显著:偏债转债的估值受到下修博弈与信用风险的影响较大,而偏股转债的估值受到赎回博弈与正股博弈的影响较大。在这两个分域中,转债本身的非线性期权特征较弱,而主动投资者对公司的深度研究与信息优势更加的明显,使得定价类因子的超额收益并不显著。反观平衡性转债,条款博弈与信用风险对其影响相对有限,而且平衡转债的期权属性最强,使得投资者更难对平衡转债进行合理定价,因此CCBA定价偏离因子可以实现显著且稳定的超额收益。• CCBA因子可以实现对赎回意愿的“中性化”:在本文开头的时候有提到过,若定价模型没有考虑到个券赎回意愿的区别,则基于定价的低估值策略易选到预期赎回意愿强的转债。我们以赎回意愿强的金融转债为例,在图表40中,CCB因子策略选出的金融转债占比要远高于市场平均。而在图表41中,CCBA因子策略选出的金融转债与市场占比接近,相当于对赎回意愿进行了“中性化”。

② 绝对定价低估策略。同时,我们可以在平衡转债增强策略中加入信用债,从而得到更加接近于绝对收益目标的策略,其中信用债仓位使用的是易方达信用债基金。我们每双周找到绝对价格低于CCBA定价的转债进行配置,个券权重最高不超过2%,整体转债仓位权重最高不超过40%,剩下的仓位配置信用债。由下图可见,该绝对收益策略从2018年开始可以实现8.7%的年化收益,在2023年也可以实现10.6%的绝对收益,波动与回撤分别仅为2.4%和1.1%。
该策略在选券的同时,也有一定的择时能力。当市场上被低估的转债数量较少时,如2022年初与2023年中,此时策略持有的转债仓位较低,因此减弱了转债高估值后可能遇到的市场回撤,策略对波动与回撤有一定的降低效果。
3.2转债与国债间的择时策略
一般来说,我们在进行转债与国债之间择时的时候,有以下两类指标可以使用,分别为:1)价格水平类,2)期权估值类。
① 价格水平类择时指标。此类指标如市场平均转债价格、纯债溢价率、YTM等。如当转债市场的平均价格较低时(纯债溢价率较低,YTM较高),说明此时转债内嵌的看涨期权价格很低,往往在权益市场大幅下跌时易出现这种情况,绝大部分转债已经跌成了虚值期权。若在此时买入转债,转债期权的delta较低,即使权益市场未来仍有下跌的可能,但是对转债价格的影响已比较有限。
我们可以使用中债3年期AA级信用债YTM与转债YTM求差值作为择时指标,从而构建简易的择时策略,当YTM差值小于历史6年中位数时,未来30日看多转债并持有100%仓位中证转债,否则持有100%仓位7-10年国债,基准设置为转债与国债的等权基准。由下图可见,该策略有较好的择时能力,可将从2008年起的年化收益由2.9%提升至6.9%。
② 期权估值类择时指标。此类指标如转债市场BS模型隐含波动率、定价偏离度等,该指标是用来衡量转债作为一个期权来看,其期权估值的高低。此处我们可以使用CCBA定价偏离度做为择时指标,当偏离度小于0时,未来30日看多转债并持有100%仓位中证转债,否则持有100%仓位7-10年国债。由下图可见,该策略也有较好的择时能力,可将从2008年起的年化收益由2.9%提升至9.4%,2018年起的年化收益由5.0%提升至10.6%。
期权估值一般常用来构建套利策略,如某个场内看涨期权估值过高(隐波过高),此时我们会选择卖空期权,同时做多delta份个股进行对冲,从而获得套利收益,而非持有国债。因此从逻辑上来说,期权估值指标更加适合做转债与股票之间的轮动与套利策略。那么为何基于期权估值指标对于转债和国债间的择时也能实现较好的效果呢?
前文我们有讨论过,转债估值中会隐含对平价的透支幅度,该透支幅度与过去一段时间的平价涨跌幅有关。由下图可见,过去一个季度的正股涨跌幅与过去一个季度的转债估值变化(CCBA定价偏离度差值)的相关系数较高,2008年起相关系数为43.9%,而2021年起相关系数已经达到了67.4%。由此可见,转债估值变化相对于正股涨跌有着很明显的动量跟随效应。因此,当转债估值处于极低位置时,权益市场往往也是长期承压且逐渐接近底部,此时若超配转债,则预期未来转债会获得“戴维斯双击”的收益,即转债估值与正股同时反弹,转债表现优于国债。
③ 转债&国债择时策略。转债&国债择时策略。我们分别将上述的两个指标相结合,构建了如下的转债&国债择时策略,策略细节如下:
• 回测时间:2008年1月至2024年2月,月度调仓再平衡。• 回测标的:1)转债:中证转债指数,2)国债:中债国债7-10年期总财富指数。1)价格水平分数:计算中债3年期AA级信用债YTM-转债YTM,并进行60日的均线平滑,使用历史6年数据计算均值方差标准化并乘以-1得到zscore,将zscore按照±1倍标准差截尾得到分数,其中计算zscore时使用的均值用中位数代替。2)期权估值分数:计算市场CCBA定价偏离度,并进行60日的均线平滑,使用历史3年数据计算均值方差标准化并乘以-1得到zscore。由于CCBA定价偏离度的中枢接近于0,因此在计算zscore时可将均值直接设置为0。最后将zscore按照±1倍标准差截尾得到分数。3)综合打分:综合打分=价格水平分数+期权估值分数,并且按照±1分截尾。2)择时策略:50%×(1+综合打分)为转债仓位,1-转债仓位为国债仓位。
下图为策略净值与表现统计。可以看出当转债市场处于高价高估值时,策略持有转债的仓位极低,如2015年与2022年初,避免了转债市场的回撤,同时策略在每次转债价格与估值的低点加仓。策略几乎每年都能跑赢基准,2008年至今实现了9.26%的年化收益,波动与回撤也有明显的降低。2022年至今也能实现4.14%的年化收益。当前转债市场处于低价低估值区间,转债配置仓位为73.7%,相对于基准超配。
风险提示:以上结论均基于历史数据和统计模型的测算,如果未来市场环境发生明显改变,不排除模型失效的可能性。
本文节选自国盛证券研究所于2024年2月8日发布的报告《可转债的赎回概率调整定价模型》,具体内容请详见相关报告。
梁思涵 S0680522070006 [email protected]
林志朋 S0680518100004 [email protected]
刘富兵 S0680518030007 [email protected]
特别声明:《证券期货投资者适当性管理办法》于2017年7月1日起正式实施。通过微信形式制作的本资料仅面向国盛证券客户中的专业投资者。请勿对本资料进行任何形式的转发。若您非国盛证券客户中的专业投资者,为保证服务质量、控制投资风险,请取消关注,请勿订阅、接受或使用本资料中的任何信息。因本订阅号难以设置访问权限,若给您造成不便,烦请谅解!感谢您给予的理解和配合。
重要声明:本订阅号是国盛证券金融工程团队设立的。本订阅号不是国盛金融工程团队研究报告的发布平台。本订阅号所载的信息仅面向专业投资机构,仅供在新媒体背景下研究观点的及时交流。本订阅号所载的信息均摘编自国盛证券研究所已经发布的研究报告或者系对已发布报告的后续解读,若因对报告的摘编而产生歧义,应以报告发布当日的完整内容为准。本资料仅代表报告发布当日的判断,相关的分析意见及推测可在不发出通知的情形下做出更改,读者参考时还须及时跟踪后续最新的研究进展。
本资料不构成对具体证券在具体价位、具体时点、具体市场表现的判断或投资建议,不能够等同于指导具体投资的操作性意见,普通的个人投资者若使用本资料,有可能会因缺乏解读服务而对报告中的关键假设、评级、目标价等内容产生理解上的歧义,进而造成投资损失。因此个人投资者还须寻求专业投资顾问的指导。本资料仅供参考之用,接收人不应单纯依靠本资料的信息而取代自身的独立判断,应自主作出投资决策并自行承担投资风险。
版权所有,未经许可禁止转载或传播。