机器学习模型的实践探索:在交易限制下能否有效预测股票收益?
导读
作为西学东渐——海外文献系列报告第一百五十六篇,本文推荐了Avramov D, Cheng S, Metzker L于2020年发表的论文《Machine learning versus economic restrictions: Evidence from stock return predictability》。
本文主要探讨机器学习模型在纳入实际交易限制后是否依旧能够有效预测股票收益率。具体的,本文采用了两种成熟的深度学习方法,即GKX 中的 NN3和 CPZ 方法,在全样本、剔除微盘股、有信用评级、剔除信用评级下调等四个子样本空间中分别训练上述两个深度学习模型,得出以下结论:1)在纳入实证金融学的交易限制,如采用市值加权或者剔除微盘股、财务状况不佳的公司后,机器学习模型的效果有显著降低。2)机器学习方法有着明显较高的换手率,在纳入交易成本后收益明显下降。
同时,本文从两个角度给出了应用机器学习方法的经济学支撑:1)本文研究发现基于两种深度学习信号构建的多头组合和大多数基于异象构建的多头组合有一定相似性。具体的,基于深度学习信号构建的多头组合也以小盘、价值、非流动性和上市时间较长的个股为主,具有低价格、低贝塔值、低过去一个月收益率(短期输家)、高过去 11 个月收益率(中期赢家)、低资产增长率、低股票发行量、高经营业绩、低信用评级覆盖率、低分析师覆盖率和高盈余惊喜特征;2)此外,本文测算了机器学习模型行业内选股和行业轮动带来的收益,提出与行业轮动相比,机器学习方法可能更适合应用于选股领域。
风险提示:文献中的结果均由相应作者通过历史数据统计、建模和测算完成,在政策、市场环境发生变化时模型存在失效的风险。
1、引言
截至目前,经济学家已经发现了许多能够有效预测横截面股票收益率的公司特征因子。然而,最近的不少研究对这些因子的可信度提出了质疑。Harvey、Liu和Zhu(2016年)研究了296个已公布的统计显著公司特征因子,得出的结论是其中80到158个因子的预测模型可能存在误差。此外,McLean 和 Pontiff(2016年)基于97个常见因子构建投资组合,发现此投资组合回报率样本外变低了26%。
Hou、Xue和Zhang(2018)的研究进一步表明,在剔除微盘股以及采用市值加权和1.96(2.78)的临界t统计量后,452个收益率预测因子中有65%(82%)变得不显著。此外,越来越多的证据表明,很多因子其实是从空头交易中获取了绝大部分收益。值得注意的是,近年来美国股市的结构性变化使得利用异象变得越来越困难。具体来说,自2001年要求10进位方式交易部分股票以来,由于市场流动性和套利活动的增加,大多数可预测的模式已经减弱(Chordia、Subrahmanyam和Tong,2014年)。
与这些 "挑战市场异常现象 "的文献相对应的是新出现的大量研究展示证明,利用各种机器学习方法产生的信号在投资中具有显著的盈利能力。从实际投资管理的角度来看,随着金融科技的发展,越来越多的人开始采用机器学习工具来生成预测价格变动的新信号,并开发出优于一般基金经理的新投资系统。这一趋势得到了2017年金融稳定委员会(FSB)的报告确认。
在学术研究中,机器学习的应用受到科克伦(2011年)在全美金融协会主席致辞中的推动。科克伦(2011年)认为,在存在大量噪音且高度相关的回报预测因子的情况下,传统的横截面回归和投资组合排序方法已经不能够满足应用需求,需要采用其他方法。事实上,机器学习提供了一种自然的方式来应对高相关性的收益预测问题。因为机器学习技术可以很好地适应于高维数据集,同时具有灵活的函数形式,并采用 "正则化"方法来选择模型,能够减轻过拟合偏差、发现复杂模式和隐藏关系(Gu、Kelly 和 Xiu,2019 年)(GKX)。因此,虽然单个预测信号往往会随着时间的推移而减弱,但机器学习技术仍可将多个(可能很弱)信息源组合成一个有意义的综合信号。
本文全面分析了机器学习方法能否应对实证金融学中的合理的实际交易限制,这一方向目前相关研究还较为匮乏。尤其我们研究了机器学习过程中产生的信号是否能够同时满足横截面和时间序列的交易限制。例如,在横截面中,我们通过将股票范围限制在交易成本相对较低的股票上,剔除了小盘股或陷入困境的公司;在时间序列中,我们研究了投资收益与减轻套利限制相关的市场状态的敏感性,例如高情绪、高波动性和低流动性。此外,我们从两个角度对“黑箱子”的机器学习方法进行经济学角度的支撑论证。
为了完成上述研究,我们主要关注两种能很好地处理金融数据的深度学习方法。我们首先实现了 GKX 中具有三个隐藏层(NN3)的神经网络,然后按照 Chen、Pelger 和 Zhu(2019)(CPZ)的方法,将无套利条件纳入多个连接神经网络,包括前馈网络、具有长短期记忆(LSTM)单元的递归神经网络(RNN)和生成对抗网络(GAN)。GKX 和 CPZ 都考虑了大量的企业特征和宏观经济预测因子以及非线性交互项,与其他机器学习方法和基准预测模型相比,它们都具有卓越的表现。GKX 研究的是初始模型设置,即不对股票收益、公司特征和宏观变量之间的关系施加实际交易限制,而 CPZ 则已经纳入了无套利条件,以估计随机贴现因子(SDF)和股票风险负载。除了深度学习信号,我们还采用了 Kozak、Nagel 和 Santosh(2019 年)(KNS)方法来估计 SDF。该方法旨在最小化 Hansen-Jagannathan 距离(Hansen 和Jagannathan 1991),重点关注股票投资组合(相对于 CPZ 中的个股)以及使用三重交叉验证的Ridge Regression。
本文基于1987 年至 2017 年间的大量美股样本,展开下述研究:1)我们首先复现了 GKX 和 CPZ 相关论文中展示的原始结果。根据 GKX 中的 NN3 预测收益率,等权(市值加权)多空投资组合收益率为每月 2.47%(1.56%),而根据 CPZ 的方法,每月的等权重(市值加权)长短期记忆网络投资组合收益率为每月 3.45%(2.18%)。相应的 Fama-French 6 因子调整(FF6调整)收益率分别为 2.25%(0.94%)和 3.5%(1.88%)。虽然 GKX和 CPZ 方法的市值加权投资组合收益率分别下降了 47% 和 43%,但这些收益明显、统计上显著的收益表现依旧反映出机器学习技术在创造出色业绩方面取得了巨大的成功。
在随后的纳入实际交易限制分析中,出现了几个主要结果:1)首先,在有实际交易限制的子样本中,收益可预测性的证据大大减弱。与基于所有股票的全样本结果相比,基于 GKX(CPZ)信号的市值加权投资组合的收益率在剔除微盘股后降低了 48%(62%),在剔除没有信用评级覆盖的公司后降低了46%(72%),在剔除信用状况恶化的财务困境公司后降低了 70%(64%)。剔除陷入困境的公司后,GKX 和 CPZ 方法在5%的水平上不再产生显著的(市值加权)FF6 调整回报;2)其次,基于机器学习方法构建的投资组合换手率大大高于大多数模型。因此,在交易成本合理的情况下,深度学习信号很难获得在统计和经济上有意义的风险调整后收益。我们的研究结果对于从训练样本中剔除微盘股以及考虑另一种损失函数(即对风险调整后的回报的预测误差进行市值加权(而非等权))都是稳健的。
上述基于 GKX 和 CPZ 信号的结论通过使用 KNS 方法得到进一步证实。由于 SDF 斜率系数对应于均值方差模型(MVE)构建的投资组合权重(Hansen 和 Jagannathan,1991 年),而 MVE 投资组合倾向于持有极端股票仓位(如 Green 和 Hollifield,1992 年),因此我们研究了实际交易限制对SDF构建的 MVE 投资组合的影响。我们发现,在全部股票样本中,基于SDF 构建的投资组合每月可获得3.34% 的 FF6 调整回报率,但在剔除微盘股公司后,FF6 调整收益率降至 0.9%,而在剔除财务状态不良的公司后,FF6 调整收益率降至微不足道的 0.55%。我们还发现,SDF 是基于相当极端的投资组合仓位估算的。例如,MVE 投资组合意味着在 10th (25th )百分位数下,个别异常点组合的空头头寸为 199%(91%),在 90th (75th )百分位数下,空头头寸为 169%(96%)。从实际投资管理的角度来看,这种极端头寸无法被投资者接受,而将投资范围限制在交易成本相对较低的股票上可以大大减轻股票仓位。
接下来,我们将研究通过机器学习信号预测股票收益率是否对市场状态敏感。相关经济理论提出,较少的交易摩擦和更多的套利活动应能提高价格效率。之前的研究表明,在投资者情绪高涨(Stambaugh、Yu 和 Yuan,2012 年;Avramov、Chordia、Jostova 和 Philipov,2018年)、市场波动性大(Nagel,2012 年)和市场流动性低(Chordia、Subrahmanyam 和 Tong,2014 年)的时期,基于异象构建的交易策略的盈利能力较高。与套利限制的经济学概念一致,本文证明在投资者情绪高涨、市场波动性大和市场流动性低的时期, 基于机器学习信号的投资策略(跨所有股票)的盈利能力要高得多。例如,基于 GKX 信号的月度市值加权 FF6 调整回报率在 VIX 低时仅为0.24%,而在 VIX 高时则大幅上升至 1.66%,而全样本平均值为 0.94%。剔除信用评级降低公司后,所有市场状态下的可预测性都进一步减弱,而且这两种机器学习信号在所有子时期都无法提供显著的风险调整后收益。作为对投资组合结果的稳健性检验,我们在联合回归中考虑了所有市场状态变量,结果证实机器学习信号的收益随市场条件的变化有很大不同。由于数据可用性和计算能力的提高,以及日益激烈的市场竞争和证明业绩的需要,资产管理领域的技术创新正在迅速发展。与传统的基于异象的交易策略(例如,Chordia、Subrahmanyam 和 Tong,2014 年;McLean 和Pontiff,2016 年)相比,我们进一步发现,深度学习信号可以预测横截面和纵截面的风险。一方面,这一发现支持了机器学习技术将多种微弱信息源组合成有意义的综合信号的观点。另一方面,近年来的异常回报模式仍局限于难以套利的股票。
当务之急是研究看似不透明的机器学习方法的经济学依据。我们首先研究了具有类似深度学习信号的股票是否也具有预测未来收益率的其他特征。证据显示,GKX 和 CPZ 方法识别出的股票与大多数基于市场异象的策略的个股相似,在整个样本期间以及最近几年都是如此。具体来说,机器学习策略的多头股票通常是小盘、价值、流动性差的股票,以及价格低、贝塔系数低、过去一个月收益率低(短期输家)、11 个月回报率高(中期赢家)、资产增长率低、股票发行量低、经营业绩高、信用评级覆盖率低、分析师覆盖率低、盈余惊喜高的股票。因此,尽管机器学习技术具有不透明性,但它们仍能根据公司特征识别出错误估值的股票。
我们进一步控制机器学习信号中的行业基准,并将无条件收益分解为两个部分:行业内选股收益和行业间收益。具体来说,我们根据 NN3 预测的收益率构建了三种交易策略,包括:1)无条件策略,即对市场赢家(市场输家)持有多头(空头)头寸;2)行业内策略,即对行业赢家(行业输家)持有多头(空头)头寸;3)行业间策略,即对赢家行业(输家行业)持有多头(空头)头寸。我们的研究表明,行业内策略的收益率远远高于行业间策略。具体而言,行业内策略的原始回报占无条件回报的 84%(即每月 1.81%中的 1.52%),FF6 调整后回报占 98%(即每月1.56%中的 1.52%)。此外,在剔除微盘股的子样本中,行业内策略的表现优于无条件策略,即行业内策略每月可获得 0.36% 的显著 FF6 调整回报,而无条件策略仅为 0.21%。因此,深度学习信号为选股而非行业轮动提供了信息。这与识别难以套利股票的错误定价的机器学习信号是一致的。根据行业平均值进行调整,可进一步控制同一行业内相似企业的基本面,从而更好地预测市场摩擦导致的后续修正。
总之,本文首次就机器学习方法的经济重要性和统计可靠性提供了大规模证据。我们采用了两种成熟的深度学习方法以及Ridge Regression,发现它们在考虑实证金融学中的实际交易限制后有效性明显降低,如市值加权收益和排除微盘股或财务不佳公司。这些结果在不同市场状态和最近几年都是稳健的。只要机器学习信号能预测横截面股票收益(所有股票),那么在投资者情绪高涨、市场波动性大和市场流动性低的时期,此交易策略就能获得更多收益。因此,综合证据表明,机器学习技术面临着横截面收益率可预测性的常见挑战,异常收益模式集中在难以套利的股票和套利限制较高的时期。机器学习信号还涉及极高的换手率,往往需要采取相当极端的多空仓位。最后,看似不透明的深度学习方法似乎能识别定价错误的股票,这与大多数基于异象的交易策略是一致的,而且机器学习方法能提供选股信息,而不是行业轮动信息。我们的研究结果不应被视为反对在量化投资中应用机器学习技术的证据。相反,基于机器学习的投资在资产管理方面大有可为。我们发现,在市场危机期间,它们能够减轻下行风险并提供良好的对冲。例如,在主要的市场低迷时期(如1987 年市场崩溃、俄罗斯违约、科技泡沫破裂和最近的金融危机),GKX 方法在剔除微盘股后平均每月产生 3.56% 的市值加权回报,而同期市场超额收益率为-6.91%。值得注意的是,与个别异象收益来源于空头组合不同,机器学习信号在多头头寸中往往也有利可图,并且在最近几年中仍然可行。经过行业调整后,机器学习信号的表现会进一步改善。我们的研究结果为在资产管理中采用机器学习技术的讨论提供了参考,包括新交易信号的有效性和可持续性、复杂的机器学习算法缺乏透明度,以及与金融稳定性相关的潜在监管影响。
2、研究方法与数据准备
2.1
研究方法
我们的实证分析主要借鉴了两种深度学习方法,这两种方法在预测未来股票收益方面均取得过经验上的成功。在第一种方法中,我们使用批量归一化和 Lasso 惩罚训练实现了一个前馈神经网络,该网络有三个隐藏层,每层分别有32、16 和 8 个神经元(NN3)。根据 GKX 的比较分析,NN3 模型相较其他模型展示出更优越的样本外性能。第二种方法由 CPZ提出,它结合了四个神经网络,包括两个前馈网络(FFN)和两个带有长短期记忆单元(LSTM)的循环神经网络(RNN)。每个 LSTM 与一个前馈网络相连。两个 FFN 的结果在损失函数中相互作用,形成一个最小优化问题,称为生成对抗网络(GAN)。
由于GKX 和 CPZ 都依赖于多层神经网络,因此它们都被认为是深度学习模型。GKX 研究的是简化形式设置,即不对数据施加明确的实际交易限制,而 CPZ 则采用无套利条件来估计 SDF 及其股票载荷。具体来说,CPZ 采用了一个最小损失最小化问题,将其表述为一个零和博弈。其中一方,即资产定价建模者,旨在选择性能最佳的模型,而另一方,即对手,则试图选择模型性能最差的条件。因此,CPZ 采用对抗方法来选择导致最大错误定价的时刻条件。
2.2
数据准备
应用GKX 模型的样本,投资范围包括所有 NYSE/AMEX/Nasdaq 股票,每日和每月股票数据来自证券价格研究中心(CRSP)。季度和年度财务报表数据来自COMPUSTAT数据库。本文构建了94个公司特征,这些特征已被相关论文论证为截面收益的重要预测因子,包括每年更新的预测因子(如绝对应计项目和资产增长)、每季度更新的预测因子(如现金流量和公司投资)以及每月更新的预测因子(如 12 个月动量和特异性波动率)。避免前瞻性偏差,月度特征最多延迟一个月,季度和年度特征分别延迟至少四个月和六个月。我们还考虑了基于标准行业分类(SIC)代码前两位数的 74 个行业虚拟变量,以及Welch 和 Goyal(2008 年)中的 8 个月度宏观经济预测因子,包括股息率、市盈率、股票方差、市净率、净股本扩张、国债利率、期限利差和违约收益率利差。我们不仅考虑了股票层面和行业层面的预测因子,还考虑了股票特征与宏观经济状态变量之间的交互作用(94 × 8),因此总共有 920 个预测因子。全样本期为 1957 年至 2017 年,然后本文将这一时期划分为三个子时期:18 年的训练样本(1957年至 1974 年)、12 年的验证样本(1975 年至 1986 年)以及用于样本外测试的其余 31 年(1987年至 2017 年)。本文采用拓展窗口进行训练,同时保持验证样本的大小保持不变,但依次将其向前滚动一年。对于样本外估算,我们对具有相同 NN3 架构但初始值不同的九个模型进行平均。样本外测试的最终样本由 21882 个模型组成。除了对训练样本采用扩展窗口外,我们还对训练样本(18 年)和验证样本(12 年)进行了滚动窗口实验。对训练样本使用滚动窗口或扩展窗口的结果在本质上是相同的。因此,在训练样本中增加学习并没有特别的效果。
应用CPZ的样本包括 CRSP 中的所有美国股票,这些股票具有与过去回报、投资、盈利能力、无形资产、价值和交易摩擦相关的 46 种公司特征数据。CPZ 还包括 178 个宏观经济预测因子,以及公司特征之间、公司特征与宏观经济状态之间的非线性交互作用。全样本期为 1967 年至 2016 年,分为 20 年的训练样本(1967 年至 1986 年)、5 年的验证样本(1987 年至 1991 年)以及用于样本外检验的剩余 25 年(1992 年至 2016 年)。为了保持一致性,我们也像 GKX 一样从 1987 年开始进行样本外测试。最终样本包括 7904 只股票,每月股票数量在 1933 至 2755 只之间。CPZ 样本中的股票数量较少的原因是CPZ要求所有公司特征都有完整的数据记录。为便于比较,GKX 将缺失特征设置为等于所有股票的相应中值。
对于有实际交易限制的子样本,全样本我们复刻了GKX 和 CPZ相关论文中的方法。同时,本文进一步探讨在相应叠加实际交易限制的子样本中训练模型的效果。现有文献指出,资产收益截面的异常现象主要集中在微盘股中。例如,Novy-Marx 和 Velikov(2016年)的研究表明,与其他规模组相比,微盘股在大多数异常情况下都显示出较高的夏普比率,但一旦考虑到交易成本,夏普比率就会变小很多。同理Hou、Xue和Zhang(2018 年)的研究表明,根据纽约证券交易所的断点以及采用市值加权收益率和 1.96(2.78)的临界 t 统计量剔除小盘股后,65%(82%)的异象不显著,这表明资本市场可能比以前想象的更有效。下面是我们计算的三个子样本的具体介绍。
第一个子样本不包括微盘股,一方面,相关证据表明微盘股的交易成本很高,以至于这些公司的异常现象很容易让边缘投资者无利可图。另一方面,众所周知,机器学习技术在揭示复杂模式和隐藏关系以及将多种微弱信息源组合成综合信号方面特别有用,而且在处理多重共线性方面往往比线性回归更有效(Rasekhschaffe 和 Jones,2019 年)。总之,我们要探讨的一个自然问题是,机器学习技术是否能够预测微盘股以外的横截面股票回报。
第二个子样本只包括具有信用评级公司,即在特定月份有标准普尔(S&P)长期发行人信用评级数据的公司,约 90% 的评级公司的规模都在纽约证券交易所规模百分位数的 20 位以上。与未评级公司相比,有评级公司往往是大型的价值型公司,其过往回报和流动性更高,特异性波动更低,分析师覆盖面更广。因此,我们将非评级公司排除在外,重点关注交易成本相对较低的股票。
第三个子样本对被评级公司进行了额外过滤。Avramov、Chordia、Jostova 和Philipov(2013 年、2018 年)的研究表明,市场异常情况往往集中在陷入财务困境的公司,尤其是在信用评级下调前后。他们提出的机制非常直接,陷入困境的公司显示出预测特征的极端值,如低过往回报率、高特异性波动率、高负盈利惊喜比例和高分析师离散度,因此它们容易被排序到异常投资组合的空头中。散户和机构投资者对财务困境的反应迟缓导致股票横截面出现多种异常回报。总的来说,一方面,投资者倾向于对陷入财务困境的股票定价过高。另一方面,信用评级下调与交易摩擦大幅增加有关,定价过高不容易被套利。因此,第三个子样本我们进一步剔除了信用评级下调前后的困境公司。具体而言,在评级公司中,我们进一步剔除了发行人信用评级下调前 12个月至下调后 12 个月的股票。
3、实际交易限制下的机器学习模型有效性分析

除原始投资组合回报外,本文还展示了根据:
(1) CAPM(即仅调整市场因子(MKT,定义为市值加权 CRSP 市场指数相对于 1 个月 T-bill利率的超额回报));
(2) Fama-French-Carhart 4 因子模型(FFC),包括市场因子(MKT)、规模因子(SMB,定义为小公司回报溢价减去大公司回报溢价)、账面市值因子(HML,定义为高账面市值回报溢价减去低账面市值回报溢价)(Fama 和 French,1993 年)和 Carhart(1997 年)动量因子(MOM,定义为赢家回报溢价减去输家回报溢价);
(3) Fama-French-Carhart 4 因子加 Pástor-Stambaugh(2003)流动性因子模型(FFC+PS);
(4) Fama-French 5 因子模型(FF5),包括市场因子(MKT)、规模因子(SMB)、
市净率因子(HML)、盈利能力因子(RMW,定义为稳健回报溢价减去疲软回报溢价)和投资因子(CMA,定义为保守回报溢价减去激进回报溢价)(Fama 和 French,2015 年);
(5) FamaFrench 6 因子模型(FF6),在 FF5 的基础上增加了动量因子(MOM)(Fama 和 French,2018年);
(6) Stambaugh-Yuan 4 因子模型(SY),包括市场因子(MKT)、规模因子(SMB)以及由公司管理(MGMT)和业绩(PERF)相关异常群产生的两个错误定价因子(Stambaugh 和Yuan,2017 年)。10所有估计中的标准误差都使用 Newey 和 West(1987 年)的方法进行了滞后自相关校正。
3.1
基于NN3模型预测股票收益
我们首先评估 GKX 方法的样本外收益预测性。首先,在 1987-2017 年的样本期内,所有股票的等权多空投资组合收益率为每月 2.47%(t统计量=9.03),非常显著。在对常见风险因素进行调整后,该投资策略仍保持高收益,每月风险调整后收益率介于 2.25% 和 2.74% 之间,t统计量高于7.91。其次,市值加权投资组合的收益率的表现大大减弱,但在统计上仍然显著。例如,市值加权多空投资组合的收益率为 1.56%,每月(t 统计量 = 4.53),所有因子模型的风险调整收益率介于 0.77% 和 1.89% 之间,t统计量均高于 3.03。我们的研究结果与 GKX展示的原始结果一致,与等权重结果相比,市值加权组合的所有业绩指标的平均下降 47%。最后,与空头头寸相比,预期收益最高的股票的多头头寸会产生显著的收益回报。例如,等权重(市值加权)投资组合的多头头寸每月产生 1.76%(0.78%)的显著 FF6 调整回报,而等权重(市值加权)投资组合的空头头寸回报则降至-0.48%(0.16%,不显著)。
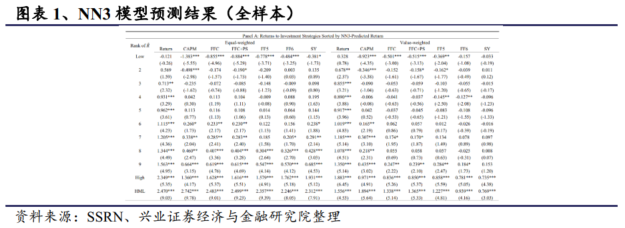
我们关于多头与空头收益对比的结论似乎与一些文献的结论不相符,相关文献记载基于异象构建的交易策略的盈利能力主要归功于空头交易(例如,Hong、Lim 和 Stein,2000 年;Stambaugh、Yu 和 Yuan,2012年;Avramov、Chordia、Jostova 和 Philipov,2013 年)。不过,也有相关观点可以支持我们的结果,即机器学习模型具有超强的能力,可以发现数据中的复杂特征,否则这些特征就会被忽视。对于共同基金和养老基金等主要关注多头头寸的机构来说,多头头寸的优秀表现尤其有价值。
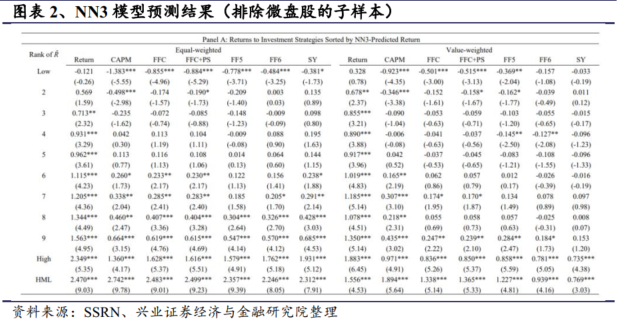
在排除小盘股的子样本中,等权重(市值加权)的多空投资组合收益率为显著的每月1.24%(1.05%)。然而,在使用FF6模型调整风险敞口后,收益率减弱,等权重投资组合每月仅为0.38%,而市值加权投资组合的收益率变得不显著。此外,NN3方法在横截面股票回报中的预测能力被Stambaugh和Yuan(2017年)的四因子充分捕捉到,导致等权重和市值加权的多空投资组合的平均α不显著。与全样本相比,排除了小盘股后,无论是在所有绩效指标上,等权重(市值加权)的收益都降低了65%(48%)。总之,当我们应用NYSE的分界点以排除小盘股,并专注于相对易于交易的股票子集时,GKX信号在统计显著性和收益表现方面都比最初的结果要弱。有人可能会说,由于我们使用整个股票池(包括微盘股)来训练机器学习算法,这种训练方案可能会偏向于检测有利的模式,尤其是微盘股。不过,本文认为,基于综合范围的训练应该能更好地捕捉子样本模式。支持这一观点的一个例子来自深度学习的另一种应用,研究人员旨在利用检测技术追踪奶牛。研究指出,在将范围从只有牛扩大到既有牛又有羊之后,效果更好。之所以能取得更好的性能,是因为各组之间存在共享属性。不过,为了安全起见,我们也根据非微小市值公司的范围来训练机器学习算法。市值加权回报率(FF6 调整回报率)为每月 1.19%(0.49%),而我们的主要结果为每月 1.05%(0.34%,不显著),而 StambaughYuan 4 因子调整(SY4 调整)收益率在统计上仍然不显著。因此,从训练样本中剔除微盘股并不会改变我们的主要研究结果。
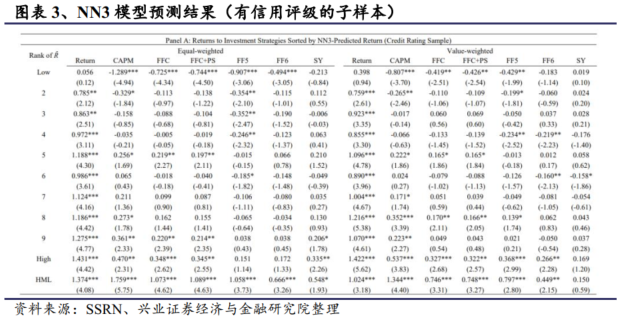
第二个子样本仅考虑具有标准普尔(S&P)长期发行人信用评级数据的公司,即仅考虑评级公司。我们根据NN3预测的收益将所有评级公司分为十分位投资组合,并按照计算持有期回报。我们将结果整理在图表3中。等权重(市值加权)的多空投资组合每月产生显著的回报,分别为1.37%(1.02%),经过FF6模型调整后的回报分别为0.67%(0.45%)每月。与全样本相比,在所有等权重(市值加权)的绩效指标上,整体下降了56%(46%)。
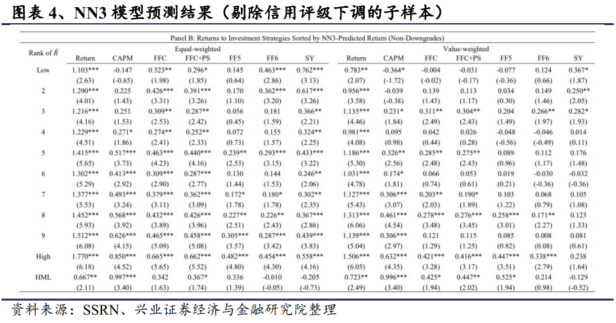
第三个子样本剔除了信用评级下调前后的财务不良企业样本。具体的,我们在评级公司中,进一步剔除了发行人信用评级下调前 12 个月至下调后 12 个月的股票。这并不是一种实时交易策略,因为我们在剔除评级下调前12 个月期间时是向前看的。不过,我们的目的是研究机器学习算法产生的交易收益率是否超出了一小部分公司(即信用评级下调前后的不良公司)。在信用状况改善或稳定期间,等权重(市值加权)多空组合每月产生 0.67% (0.72%)的显著回报,而 FF6 调整后的回报在统计上不再显著。此外,在等权重(市值加权)投资组合的 6 个风险调整回报中,只有 1 个(2 个)在 5%的临界值下仍然显著。由于我们在样本外测试中关注的是风险调整后的市值加权投资组合收益,因此我们还采用了另一种目标函数来预测 FF6 调整后的回报而非原始回报,以及最小化市值加权预测误差而非等权预测误差。这使得我们在训练和验证机器学习算法时,可以将估算结果向大盘股倾斜,并专注于预测风险调整后的回报率。在全部样本中,FF6 每月市值加权调整收益率为 0.61%,而使用 GKX 方法的收益率为0.99%。同样,在大多数有实际交易限制的子样本中,基于使用市值加权损失函数的 NN3预测阿尔法的交易收益率并不优于原始的 GKX 方法(即使用等权重损失函数的 NN3 预测回报率)。例如,按 NN3 预测阿尔法排序的市值加权多空投资组合得出的 FF6 调整回报率在剔除微型公司后每月为 0.38%(0.35%)(均在 10%的水平上显著),在剔除没有信用评级覆盖的公司后每月为 0.34%(显著 0.51%),在剔除信用评级下调前后陷入财务困境的公司后每月为 0.13%(0.3%)(均不显著)。因此,我们的主要发现对于偏重于预测大盘股风险调整收益的替代目标函数是稳健的。
3.2
基于CPZ模型预测股票收益
在 1987-2016年的样本期内,所有股票的多空组合收益率(FF6 调整后收益率)都非常显著,且收益表现较好,等权重组合的月收益率为 3.45% (3.5%),市值加权组合的月收益率为 2.18% (1.88%),与我们之前的研究结果类似。
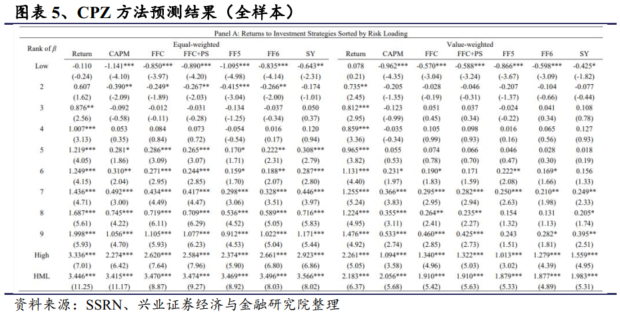
剔除微盘股后,收益表现显著减弱。等权重投资组合的多空组合收益率(FF6 调整后回报率)下降至每月1.59%(1.18%),市值加权投资组合的多空组合收益率下降至每月 1.08%(0.56%)。在所有业绩衡量指标中,剔除微盘股的子样本的等权重(市值加权)收益率比全样本低 60%(62%)。

有信用评级公司的等权重多空策略每月收益率为 1.52%,FF6 调整后收益率为 1.28%。此外,市值加权交易策略的月收益率为 0.81%,FF6 调整后的收益率在统计上不再显著。

如果进一步剔除信用评级下调的公司,等权重投资组合的多空组合月收益率(FF6 调整后回报率)为 1.41%(1.05%),t 统计量为 0.92%(0.58%)。在所有业绩衡量指标中,与全样本相比,评级公司子样本的等权(市值加权)交易收益率要低 60%(72%),如果我们进一步剔除信用状况恶化的公司,则要低 65%(64%)。因此,在存在合理实际交易限制的情况下,投资回报率会进一步下降。
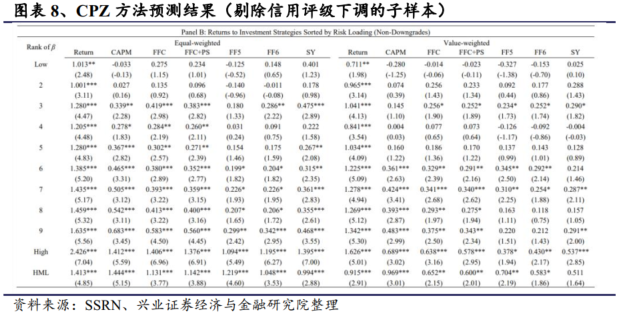
总体而言,创新的机器学习技术面临着横截面回报可预测性的通常挑战,异常回报模式集中在相对难以套利的股票上。一旦我们施加实证金融学中常见的实际交易限制,如剔除微盘股或财务困境样本,基于 GKX 和 CPZ 深度学习信号的交易收益率往往会在风险调整后消失。
3.3
机器学习投资组合的非正态性和换手率
除了样本外收益的可预测性,投资者在应用投资策略时还应关注其他潜在风险和成本。以单个异象为例,过去的研究表明,部分异象的收益很容易出现大幅回撤。Daniel 和 Moskowitz(2016 年)的研究表明,动量策略偶尔会出现大幅崩盘。Arnott、Harvey、Kalesnik 和Linnainmaa(2019 年)的最新研究表明,在 14 个流行因子中,有 9 个是肥尾因子,且下行时不对称。此外,交易成本也会大大降低异常回报。Novy-Marx 和 Velikov(2016)发现,在考虑交易成本后,虽然大多数低换手率和中换手率策略仍然有利可图,但是高换手率策略几乎很难获得显著为正的超额收益。
在本小节中,我们将探讨与机器学习投资组合相关的下行风险和换手率影响。我们根据 GKX 和 CPZ 中的深度学习信号将股票排序为十等分组合。由于数量众多但总市值极小的股票可能会对等权重投资组合收益长盛较大影响,而市值加权能准确捕捉投资者所经历的总财富效应(Fama,1998 年),因此我们在后面的分析中将重点放在市值加权结果上。我们计算每个十分位数投资组合的市值加权持有期收益率,并计算多空投资交易策略表现,即做多前十分位数的股票,做空后十分位数的股票。我们还将市场投资组合作为基准,市场超额收益定义为市值加权 CRSP 市场收益超过 1 个月 T-bill利率的部分。我们展示了年化夏普比率、月度收益的偏度和超额峰度、最大回撤率、平均回撤率、月度回报的偏度和超额峰度、危机期间的月回报率,以及多空机器学习组合和市场组合的月换手率。


下表中列出了按 NN3 预测收益率排序的投资组合(GKX)、按 SDF 风险载荷排序的投资组合(CPZ)和按市场投资组合排序的投资组合(C)的结果。我们展示了全部样本以及剔除微盘股、无评级公司和信用评级下调的子样本的结果。其中所有收益率均按每年10%的波动率缩放,以便于在不同样本和方法之间进行比较。
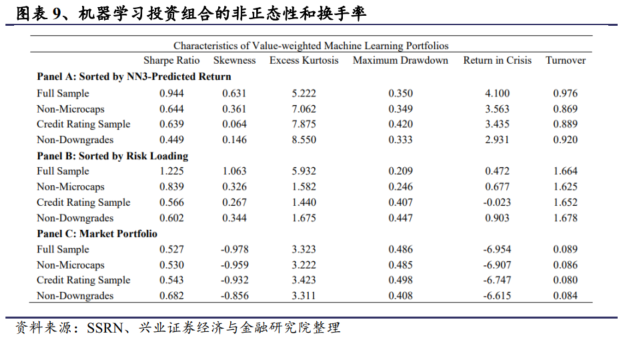
首先,GKX(CPZ)方法在全样本中的年化夏普比率为 0.94(1.23),而市场投资组合的年化夏普比率为 0.53。虽然机器学习方法在除信用评级下调之外的大多数子样本中的表现仍优于市场组合,但施加实际交易限制会大大降低夏普比率。其次,在全部样本和所有三个子样本中,GKX(CPZ)方法的偏度和峰度均为正值,而市场投资组合的偏度为负值。第三,在全样本中,GKX(CPZ)方法的最大回撤率为 35%(21%),而市场投资组合的回撤率更大,为 49%。在大多数子样本中,这两种方法的回撤率也相对小于市场投资组合。此外,在危机期间,基于深度学习的交易策略的平均收益大多为正,其中 GKX 方法的平均收益为每月 2.93% 至 4.1%,CPZ 方法的平均收益为每月-0.02% 至 0.9%。与同期近 -7%的平均市场回报率相比,是一个重大进步。综合证据表明,机器学习方法能够降低下行风险,保护投资者免受极端暴跌的影响。
GKX 和 CPZ 方法在重新平衡投资组合时都需要较高的换手率。GKX方法的多空组合月换手率在 87% 到 98% 之间,CPZ 法的月换手率在 162% 到 168% 之间,这意味着 GKX 法的单边换手率(多头和空头的平均换手率)至少为 44%,CPZ 法的单边换手率至少为 81%。从这个角度来看,规模和价值等低换手率策略的月单边换手率通常低于 10%,失败概率和特异性波动率等中换手率策略的相应数字在 14% 至 35% 之间,而短期反转和季节性等高换手率策略的月单边换手率则在 90% 以上(Novy-Marx 和 Velikov,2016 年)。根据 Novy-Marx 和 Velikov(2016 年)的研究,交易成本占市值加权投资组合每月单边换手率的 1%以上,超额收益的统计意义将按比例降低。也就是说,如果策略的多头每月换手率为 50%,则已实现的多空收益率每月至少比总收益率低 0.5%。之前文中指出,GKX 方法在全样本中产生的市值加权月收益率(FF6 调整后回报率)为 1.56%(0.94%),剔除微盘股后为 1.05%(不显著的 0.34%)。CPZ 方法在全样本中产生的市值加权月回报率(FF6 调整后回报率)为 2.18%(1.88%),剔除微盘股后为 1.08%(0.56%)。因此,交易成本大大降低了基于 GKX(CPZ)方法的交易策略的总收益率,至少降低了 0.44%(0.81%)。综上,在存在合理交易成本的情况下,这两种深度学习方法都很难取得在统计和经济学上有意义的风险调整绩效。
3.4
SDF-Implied Tangency组合的表现和权重
除了基于深度学习的信号外,我们还考虑了 KNS 提出的机器学习方法。与 CPZ 一样,KNS方法也结合了无套利条件来估计 SDF。CPZ 使用个股估算 SDF,而 KNS 则侧重于代表基于特征的交易策略的股票投资组合。我们首先根据 GKX 采用的 94 个预测特征组成投资组合。本文按照 KNS 的方法对每个特征进行量纲转换,并对每个量纲转换后的特征进行归一化处理。然后,我们构建多空投资组合,并计算市值加权组合回报。我们以每日收益率为依据,将样本分为两个子时期。第一个时期为 1964 年 9 月至 2004 年 12 月,用于样本内估计。第二个时期为 2005 年1 月至 2017 年 12 月,为样本外测试期。

为了纳入我们提出的实际交易限制,我们对全部样本和排除微盘股公司、无评级公司或财务困境公司的三个子样本的 SDF 进行了四个版本的估计。由于 SDF 斜率系数与 MVE 投资组合的权重相对应,我们使用 2005 年以前样本估计的 SDF 系数来计算隐含的样本外 MVE 投资组合收益率(与市场投资组合正交)。投资组合收益率的标准差被重新调整为等于总体市场指数超额收益率的样本内标准差。
下面是经 CAPM 和 FF6 模型调整的月度超额收益率。由于投资组合与市场正交,因此SDF 估算的 MVE 投资组合回报已经过 CAPM 调整。FF6 调整回报率是通过将 基于SDF 构建的 MVE投资组合收益率与基准投资组合收益率进行回归估算得出的,其中基准投资组合收益率是根据2005 年之前的五个非市场因素估算出的非规范化 MVE 投资组合权重。我们还展示了年化夏普比以及 MVE投资组合权重(即 SDF 斜率系数)在 94 个特征中的量化分布。
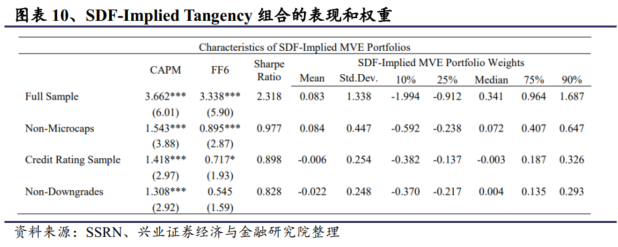
首先,我们基本复现了 KNS 的结果。SDF 估算的 MVE 投资组合表现相当出色,年化夏普比率为 2.32,CAPM 和 FF6 调整后的月回报率均超过 3%。如前所述,在 KNS 中,我们使用了一组不同的特征,此外,在现阶段,我们并不剔除小盘股。接下来,我们证实了我们的发现,即施加实际交易限制会削弱机器学习方法的效果。例如,SDF-Implied Tangency投资组合在剔除小盘股后,每月的 FF6 调整回报率为 0.9%,而在剔除微盘股后,每月的 FF6 调整回报率仅为 0.55%,年化夏普比率也降至0.98 (0.83)。
值得注意的是,投资组合权重在 94 个预测因子中显示出很高的分散性,并且经常出现极端值,这在实践中是不可行的。例如,SDF 构建的 MVE 投资组合要求在 10th (25th)百分位数时对单个预测因子持有-199%(-91%)的空头头寸,在 90th (75th )百分位数时持有169%(96%)的多头头寸。因此,从实际角度来看,该投资组合无法实现。然而,施加实际交易限制可以大幅降低极端头寸的概率。同时,SDF 估算的 MVE 投资组合要求在 25th 百分位数时对单个预测因子持有 -24% ( -22%)的空头头寸,而在 75th 百分位数时,如果剔除微盘股(财务不佳公司),则需要持有 41% (14%)的多头头寸。
本节提供的综合证据表明,机器学习技术面临着横截面回报可预测性这一常见挑战。我们使用 GKX 和 CPZ 中提倡的两种深度学习方法以及 KNS 方法生成的预测信号分析样本外交易收益。一旦我们应用纽约证交所的断点来剔除小盘股,在所有业绩指标上,市值加权交易收益率比 GKX(CPZ)最初论文给出的等权全样本结果低 71%(78%)。同样,剔除财务不佳的公司后,市值加权交易收益比全样本的等权收益低 82%(80%)。此外,在两个深度学习信号的 5%阈值下,市值加权 FF6调整回报率仅在三个子样本(即剔除微型公司、非评级公司和不良公司)中的一个子样本中显著。由于基于机器学习的交易策略需要相对较高的投资组合换手率,以及在SDF-Implied Tangency组合中采取极端的多空仓位,投资者应进一步降低对可实现业绩的预期。总之,实际交易限制在评估新的机器学习方法是否有效和可实时利用方面发挥着重要作用。我们的研究结果与 Arnott、Harvey和 Markowitz(2018 年)提出的担忧不谋而合,并证实了在评估机器学习技术时回测需要纳入一些相应实际考虑(如我们语境中的实际交易限制)的必要性。
3.5
时变收益的预测性
上述结果提供了一个相当明确的信息,即在交易成本相对较低的股票中,机器学习信号的横截面收益可预测性会降低。我们接下来要研究的是,股票收益率的可预测性是否也会随时间而变化。具体来说,我们将交易收益与市场条件的变化联系起来,研究最近几年的可预测模式变动。
1)基于投资组合收益的分析
经济理论认为,减少交易摩擦和增加套利活动应能提高价格效率。因此,在存在套利约束限制的情况下,基于异象的交易策略应该更有利可图。许多关于异象的现有证据通常都支持这一观点。Stambaugh、Yu 和 Yuan(2012 年)发现,在情绪高涨时期,市场异常现象更强。他们将情绪效应归因于卖空约束,而卖空约束在投资者情绪高涨时尤其起作用。此外,Miller(1977)的论点也表明,在投资者对基本面估值可能存在分歧且卖空约束存在时,高估在情绪高涨时期会盛行。Avramov、Chordia、Jostova 和 Philipov(2018 年)进一步表明,整个市场的情绪和公司层面的财务困境共同推动了股票和公司债券的定价过高。其次,大量理论研究预测,由于资金约束收紧和风险偏好降低,较高的波动性会降低做市商的流动性提供能力(Gromb 和Vayanos,2002 年;Brunnermeier 和 Pedersen,2009 年;Adrian 和 Shin,2010 年)。因此,在金融市场动荡时期,由于流动性枯竭,异象(尤其是与流动性提供相关的因子的收益)可能会增加(Nagel,2012 年)。最后,Chordia、Subrahmanyam 和 Tong(2014 年)发现,由于套利活动的增加,近期股市流动性的增加与股票回报异常的减弱有关。
首先,我们根据投资者情绪、市场波动性和市场流动性的状况,研究机器学习投资组合在不同时期的收益。我们考虑以下市场状态变量:1) 投资者情绪(SENT),定义为 Baker 和 Wurgler(2007 年)的月度投资者情绪;2) 已实现市场波动率(MKTVOL),定义为一个月内 CRSP 每日市值加权指数收益率的标准差;3) 隐含市场波动率(VIX),定义为标准普尔 500 指数期权隐含波动率的月度 VIX 指数;4) 市场非流动性(MKTILLIQ),定义为某月所有 NYSE/AMEX股票的股票级 Amihud(2002)非流动性的市值加权平均值。
我们根据整个样本期间 SENT(MKTVOL,VIX)的中位数断点,将整个样本分为两个子时期,即投资者情绪高涨与低落(已实现市场波动率,隐含市场波动率)时期。与其他市场状态变量不同的是,由于 2001 年 1 月的十进制大大降低了交易成本,我们分别获得了 2001 年前和 2001 年后市场流动性不足的中值分界点。
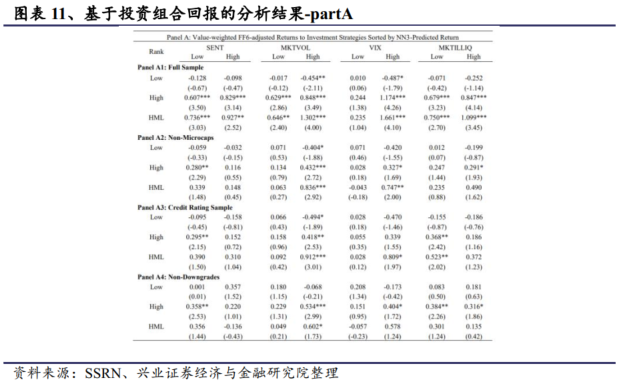
我们计算每个十分位投资组合的市值加权持有期收益率,并计算多空投资组合表现,即做多前十分位的股票,做空后十分位的股票,结果见下图表。在图表11中,十分位数投资组合按 NN3 预测收益(GKX)排序,而在图表12 中,十分位数投资组合按 SDF 的风险负荷(CPZ)排序。我们展示了全样本(面板 A1 和 B1)以及剔除微盘股(面板 A2 和 B2)、无评级公司(面板 A3 和 B3)和信用评级下调公司(面板 A4 和 B4)后的子样本的结果。为简洁起见,我们仅列出了空头和多头十分位数投资组合的 FF6 调整后收益率以及多空交易策略("HML")表现。
从 NN3 开始,有几个发现值得注意。首先,除低 VIX 期外,所有多空组合交易收益率在所有子期都在 5%的水平上显著。在投资者情绪高涨、市场波动率高和市场流动性低的时期,该投资策略也更有利可图。其次,在所有市场状态变量中,已实现市场波动率和隐含市场波动率在解释随时间变化的回报率可预测性方面发挥着重要作用。在 MKTVOL(VIX)较低时,市值加权的 FF6 调整回报率为每月 0.65%(0.24%,不显著),而在 MKTVOL(VIX)较高时,则大幅上升至每月 1.3%(1.66%),而图表11的 面板 A 中的全样本平均值为 0.94%。第三,如果我们继续分析剔除小盘股或无评级公司的子样本,那么在市场高波动率时期, 投资策略仍然更有利可图(就已实现波动率和隐含波动率而言)。最后,考虑到不包括信用评级下调的子样本,在 5%的水平上,没有一个子时期显示出显著的多空交易收益率。最后一个证据加强了以下观点,即在剔除信用评级下调前后的受困公司后,多空交易收益率在 5%的水平上并不显著。评级下调后,GKX 信号在整个样本期内未能提供显著的 FF6 调整回报(每月 0.21%,并不显著)。而对于按 SDF(CPZ)的风险负荷排序的十等分投资组合,在全样本中,我们观察到所有子期(B1)的多空交易收益率均在 5%的水平上显著,并且在投资者情绪高涨、市场波动性(已实现波动率和隐含波动率)高和市场流动性低的时期,该投资策略表现优异。然而,在 B2至 B4 时期的所有三个子样本中,只有一个子期在 5%的水平上显示出显著的多空交易收益率。施加实际交易限制后的收益预测能力较弱,这与全样本结果一致,即一旦剔除非评级公司和信用评级下调的公司,每月 FF6 调整后的收益在 5%的水平上不显著。未展示的结果进一步表明,机器学习投资组合在不同市场状态下显示出相似的换手率。总体而言,我们发现深度学习信号可以预测所有股票的横截面收益率,尤其是在投资者情绪高涨、市场波动大和市场流动性低的时期--这与套利限制的经济概念相一致。然而,施加实际交易限制会削弱所有市场状态下的收益预测能力,深度学习信号在整个样本期间以及各种市场状态下都无法提供有意义的风险调整绩效。

2)时间序列回归
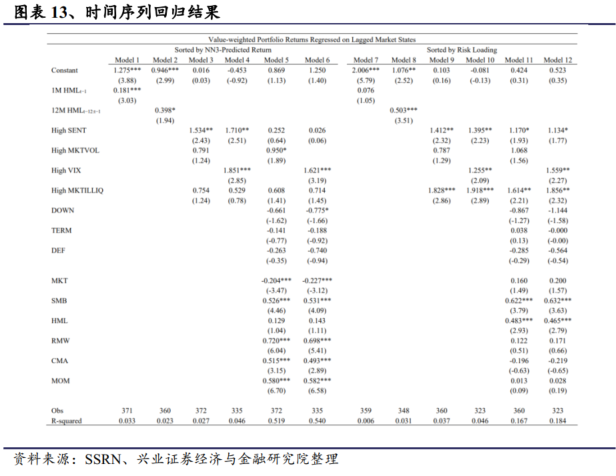
接下来,我们进行时间序列回归分析,共同考虑所有市场状态变量。我们还明确控制了市场状态和宏观经济条件的其他替代变量。由于深度学习信号的收益预测性在有实际交易限制的子样本中会大大减弱,因此我们将重点放在包括所有股票在内的全样本上进行时间序列分析。


下表结果显示在市场高波动期,基于 NN3 预测的 GKX 回报率的交易收益率在已实现波动率和隐含波动率方面都更高。市场波动性的预测效果也超越了投资者情绪、市场流动性、宏观经济变量和风险因素(模型 5 至 6)。当按 CPZ 信号对十等分投资组合进行排序时,模型9 至 12 展示了类似的结果。在投资者情绪高涨、隐含市场波动率高和市场流动性低的联合模型中(模型 12),多空投资组合的回报率更高。
3)近年来回报的可预测性
自 2000 年代以来,美国股票市场发生了巨大的结构性变化,如引入十进制和改善市场流动性、更多机构投资者的参与、更好地获取更广泛数据的途径、金融技术的发展以及采用先进的定量分析等。Chordia、Subrahmanyam 和 Tong(2014 年)的研究表明,2001 年 1 月十进制实施后,大多数市场异象情况都有所减少,由 12 种市场异象情况组成的交易策略的平均收益和夏普比率减少了一半以上。与投资者从学术出版物中了解错误定价的情况一致,McLean 和 Pontiff(2016年)的研究表明基于市场异象的投资组合回报率在样本外低 26%,在推出后低 58%。
随着大数据和量化模型在资产管理领域的日益普及,我们研究了近年来机器学习技术是否仍然有意义。我们根据深度学习信号将股票排序为十分位投资组合。
我们通过做多顶部十分位数的股票和做空底部十分位数的股票来实施多空投资交易策略,并计算2001 年后的持有期收益率。
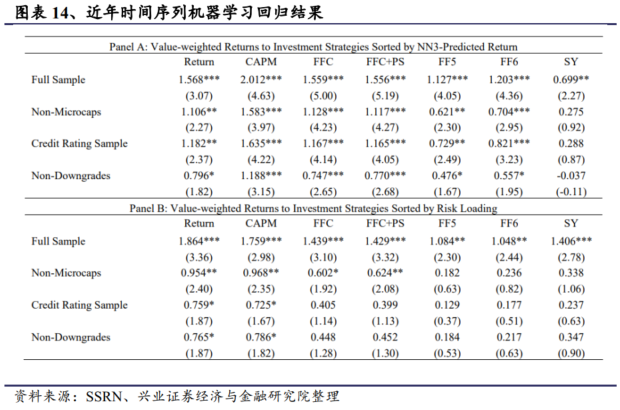
表中展示了多空组合的市值加权表现。十分位投资组合按 NN3 预测收益率(GKX)排序。我们从 1987 年到 2017 年的主要研究结果在 2001 年之后的时期依然保持不变。所有股票的市值加权多空投资组合收益率为每月1.57%,经 FF6 模型调整后为 1.2%。经济规模也与整个样本期相当,即原始回报率为 1.56%,FF6调整后回报率为 0.94%。此外,近年来机器学习信号仍能预测非微型公司和评级公司的股票收益截面。将重点转移到最严格的子样本(不包括信用评级下调),原始回报率和 FF6 调整回报率在5%阈值下不再显著。
下图展示了按 SDF(CPZ)风险负荷排序的十等分投资组合的类似结果。所有股票的市值加权多空组合收益率为每月 1.86%,经 FF6 模型调整后为 1.05%。经济规模略低于 1987 年至2016 年期间,即原始回报率为 2.18%,FF6 调整后回报率为 1.88%。近年来,施加实际交易限制进一步削弱了样本外收益率的统计和经济预测能力,在剔除微型公司、非评级公司或信用评级下调的子样本中,我们没有检测到显著的 FF6 调整收益率。总体证据表明,在全样本中,深度学习信号继续预测近年来的横截面股票回报率。换句话说,与个别异常现象不同,机器学习信号的交易收益率并没有大幅下降。这表明机器学习方法有能力将多个可能较弱的信号整合成一组有意义的信息。另一方面,异常回报模式仍局限于难以套利的股票,因此从业者在利用机器学习算法进行实时交易时应保持谨慎。
4、两维度解析机器学习方法的经济学基础
Cochrane(2011)指出,传统的回归分析和组合排序可能不足以处理大量的预测变量。对此,机器学习提供了一种自然的方法来适应高维预测集和灵活的函数形式,并采用 "正则化 "方法来选择模型和减轻过拟合偏差(GKX)。然而,深度学习模型本质上是不透明的,通常被称为 "黑盒子"。在本节中,我们将重点关注全样本,并就机器学习方法中回报可预测性的经济驱动力提供证据。具体来说,我们研究了具有类似机器学习信号的股票是否也具有其他可预测未来回报的特征。我们还对行业基准进行了控制,并研究了收益率可预测性的来源。
4.1
机器学习投资组合的股票特征
在每个月的月底,股票按深度学习信号排序为十分位数。然后,我们计算每个月末股票特征的等权平均值。大部分股票特征来自 GKX 中使用的公司层面预测因子,包括绝对应计、对数上市时间、资产增长、贝塔值、市价账面值、∆ 流通股、公司投资、股息价格比、毛利率、特异性回报、波动率(IdioVol)、对数(流动性不足)、杠杆率、12M 动量、资产回报率(ROA)和股本回报率(ROE)。我们还考虑了其他公司特征,如对数(价格)、对数(规模)、1M 回报率、评级公司百分比(%Rated)、信用评级、分析师覆盖率、分析师离散度和标准化意外收益(SUE)。我们从机构经纪人估算系统(I/B/E/S)中获取分析师预测数据。结果如下表。
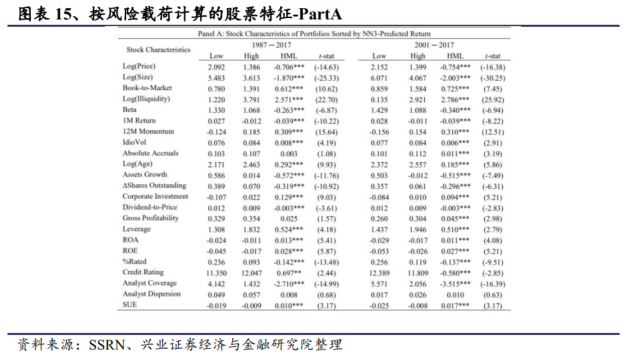
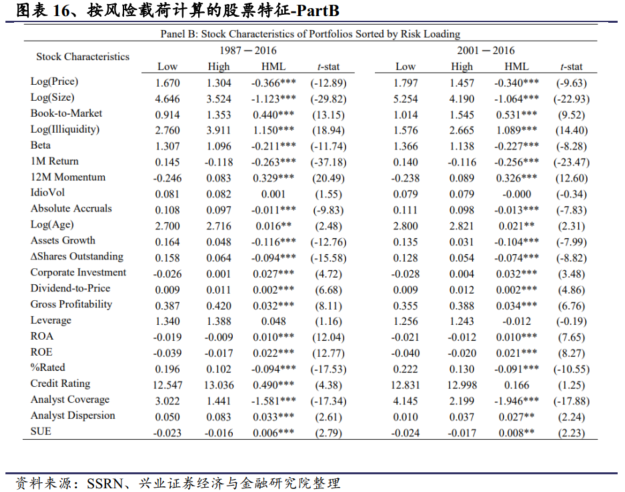
在上表结果中,十分位投资组合分别按照 NN3 预测收益率(GKX)和 SDF 风险载荷(CPZ)排序。为简洁起见,本文只列出Bottom和Top十分位数投资组合的股票特征,以及多空十分位数投资组合的价值差("HML")。我们考虑了从 1987 年到 2017 年的整个样本期以及 2001 年后的样本期,并展示Newey 和 West(1987 年)调整后的 t 统计量(4 个滞后期)。有几个发现值得注意。
首先,GKX 和 CPZ 方法都能识别出符合大多数基于异象交易策略的股票。这些结果对全样本和 2001 年后时期都是稳健的。例如,在基于深度学习的交易策略中,处于多头位置的股票通常是小盘股、价值股、非流动性股,它们具有低价格、低贝塔值、低 1 个月回报率(短期输家)、高 11 个月回报率(中期赢家)、低资产增长率、低股票发行量、高 ROA 和 ROE 的经营业绩、低信用评级覆盖率、低分析师覆盖率和高盈利惊喜。因此,尽管机器学习技术具有不透明性,但它能识别出具有坚实经济基础的错误定价股票。
其次,机器学习信号的交易方向与个别异常特征相反的情况有两种。其一,GKX 和 CPZ 方法都在企业投资较高的股票中持有多头头寸,而就个体而言,这预示着平均较低的未来回报率(Titman、Wei 和 Xie,2004 年)。其次,GKX 方法在特异性波动率高的股票上建立多头头寸。未来回报可能与公司投资或特质波动性都不是线性关系,回报预测性可能受到其他相关公司特征或宏观条件的影响。正如 Titman、 Wei 和 Xie(2004 年)所指出的,投资与回报的负相关关系在现金流较高、负债率较低的企业中更为突出。Stambaugh、Yu 和 Yua(2015)的研究也表明,特异波动与收益的关系在定价过高的股票中为负,但在定价过低的股票中则转为正。横截面中这种复杂且往往模糊的模式确实凸显了采用机器学习技术的优点,因为它们可以从大量相关特征中提炼信息。最后,未展示的结果证实,我们的主要发现对投资者情绪、市场波动性和市场流动性等市场状态是稳健的。
4.2
行业内与行业间的预测收益对比
同一行业内企业的收益率具有高度相关性,因为它们可能受到共同技术冲击、运营和监管环境变化以及特定行业对某些产品和服务的供求关系的影响。本文之前的研究结果表明,深度学习信号大多能预测难以套利股票的未来回报。如果此类交易信号捕捉到了市场摩擦导致的暂时性错误定价和随后的修正,那么匹配同行业中的类似公司就为控制公司基本面和了解回报可预测性的来源提供了一个自然框架。对行业基准的控制还能告知机器学习方法是专门从事选股还是行业轮动,即对类似公司进行聚类并对行业组合进行交易。



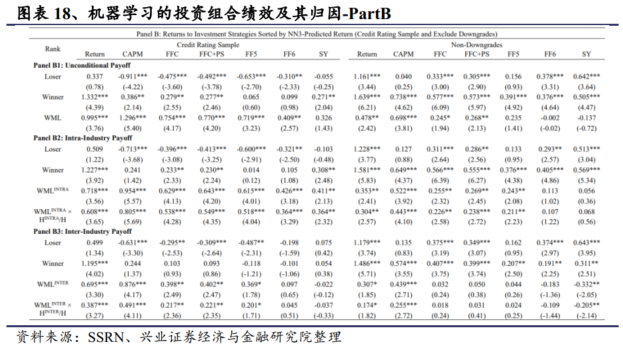
其中表 A 是全样本和剔除小盘股的子样本,表B 是剔除无评级公司或信用评级下调的子样本。在表A1和B1中,我们展示了无条件策略下赢家和输家投资组合的收益率,其中赢家(输家)包括根据 GKX 中 NN3 预测收益率有望跑赢(跑输)市场平均水平的股票。我们还通过做多赢家股票和做空输家股票来实施交易策略。零投资交易收益率的计算方法是赢家减去输家。
在1987-2017 年的样本期内,所有股票的平均多空组合回报率为每月1.81%,经 FF6 模型调整后为 1.56%,回报率显著。此外,原始回报率为每月 0.92%(0.48%),FF6 调整后的回报率在剔除微盘股(信用评级下调)的子样本中不显著。这项基于所有股票的分析证实了我们从极端十等分组合中得出的主要结论,即机器学习信号在廉价交易股票子集中大幅减弱。
在表 A2 和 B2 中,我们展示了行业内策略的赢家和输家投资组合的收益率,根据 NN3 预测的收益率,赢家(输家)股票的表现有望超过(低于)行业平均水平。我们还通过做多赢家股票和做空输家股票来实施交易策略。多空投资交易

5、结论
近年来,机器学习技术在资产定价研究和实际投资管理中被广泛采用。本文首次证明了机器学习方法的经济重要性和统计可靠性。本文采用了两种成熟的深度学习方法,即GKX 中的 NN3 预测收益率和 CPZ 中的对抗方法。我们发现,这些方法在考虑实证金融学中的标准实际交易限制(如计算市值加权收益、剔除微盘股公司或信用风险较高公司)后表现明显降低。在全部样本中,GKX(CPZ)方法的市值加权投资组合回报与等权加权回报相比,在所有业绩衡量指标中下降了 47%(43%)。一旦我们进一步纳入的实际交易限制,基于 GKX (CPZ) 信号的市值加权投资组合回报率在剔除微盘股后会降低 48%(62%),在剔除无评级公司后会降低 46%(72%),在排除信用评级下调前后的不良公司时会降低 70%(64%)。类似的证据也适用于 KNS 倡导的基于Ridge Regression的机器学习方法。值得注意的是,机器学习方法同时具有较高的高换手率,在存在交易成本的情况下,很难具备alpha。
在深度学习信号预测横截面股票回报的范围内,该交易策略在套利限制增加的时期(如投资者情绪高涨、市场波动大和市场流动性低)表现更佳。我们重点研究了不包括信用评级下调的最严格子样本,结果表明深度学习信号无法提供有意义的风险调整回报。
不过,我们的研究结果不应被视为反对在量化投资中应用机器学习技术的证据。相反,基于机器学习的交易策略在资产管理方面大有可为。机器学习模型具有卓越的能力来检测数据中的复杂特征,并将多个(可能是微弱的)信号组合成一组有意义的信息,与这一理念相一致,我们发现基于机器学习的交易策略显示出较低的下行风险,并在危机期间继续产生正收益。虽然单个异常点的盈利能力主要由空头头寸驱动,并且在最近几年经常消失,但深度学习信号在多头头寸中产生了可观的利润,并且在 2001 年后的时期仍然可行。这对实时交易、风险管理和只做多头的机构尤其有价值。
本文还研究了两种机器学习方法的经济学依据。我们发现,这两种深度学习信号识别的股票与大多数基于异象构建的策略选择出的股票一致。具体来说,在基于机器学习的交易策略中,多头组合也以小盘、价值、非流动性和上市时间较长的个股为主,它们具有低价格、低贝塔值、低过去一个月回报率(短期输家)、高过去 11 个月回报率(中期赢家)、低资产增长率、低股票发行量、高经营业绩、低信用评级覆盖率、低分析师覆盖率和高盈利惊喜等特质。此外,与行业轮动相比,机器学习方法可能更适合选股。
这些发现有助于我们理解机器学习在资产管理中的应用。众多证据表明,机器学习技术面临着横截面回报可预测性的通常挑战,超额收益主要来自难以套利的个股和套利限制较高的时期。因此,在评估新开发的机器学习方法是否成功时,必须考虑常见的实际交易限制因素。
风险提示:文献中的结果均由相应作者通过历史数据统计、建模和测算完成,在政策、市场环境发生变化时模型存在失效的风险。
参考文献
【1】Adrian, T., and H. S. Shin.2010.Liquidity and leverage.Journal of Financial Intermediation 19:418-437.
【2】Ali, A., L.-S. Hwang, and M. A. Trombley. 2003. Arbitrage risk and the book-to-market anomaly. Journal of Financial Economics 69:355–373
【3】Amihud, Y. 2002. Illiquidity and stock returns: Cross-section and time-series effects. Journal of Financial Markets 5:31–56
【4】Arnott, R., C. R. Harvey, V. Kalesnik, and J. Linnainmaa. 2019. Alice’s adventures in factorland: Three blunders that plague factor investing. Working Paper.
【5】Arnott, R., C. R. Harvey, and H. Markowitz. 2018. A backtesting protocol in the era of machine learning. Working Paper.
【6】Avramov, D., S. Cheng, and A. Hameed. 2016. Time-varying liquidity and momentum profits. Journal of Financial and Quantitative Analysis 51:1897–1923.
【7】Avramov, D., T. Chordia, G. Jostova, and A. Philipov. 2009. Dispersion in analysts’ earnings forecasts and credit rating. Journal of Financial Economics 91:83–101
【8】Avramov, D., T. Chordia, G. Jostova, and A. Philipov. 2013. Anomalies and financial distress. Journal of Financial Economics 108:139–159.
【9】Avramov, D., T. Chordia, G. Jostova, and A. Philipov. 2018. Bonds, stocks, and sources of mispricing. Working Paper
【10】Baker, M., and J. Wurgler. 2007. Investor sentiment in the stock market. Journal of Economic Perspectives 21:129–151
【11】Balakrishnan, K., E. Bartov, and L. Faurel. 2010. Post loss/profit announcement drift. Journal of Accounting and Economics 50:20–41.
【12】Bandyopadhyay, S. P., A. G. Huang, and T. S. Wirjanto. 2010. The accrual volatility anomaly. Working Paper
【13】Bhandari, L. C. 1988. Debt/equity ratio and expected stock returns: Empirical evidence. Journal of Finance 43:507–528.
【14】Bianchi, D., M. Büchner, and A. Tamoni. 2019. Bond risk premia with machine learning. Working Paper
【15】Brunnermeier, M. K., and L. H. Pedersen. 2009. Market liquidity and funding liquidity. Review of Financial Studies 22:2201–2238.
【16】Carhart, M. M. 1997. On persistence in mutual fund performance. Journal of Finance 52:57–82
【17】Cella, C., A. Ellul, and M. Giannetti. 2013. Investors’ horizons and the amplification of market shocks. Review of Financial Studies 26:1607–1648
【18】Chen, L., M. Pelger, and J. Zhu. 2019. Deep learning in asset pricing. Working Paper
【19】Chordia, T., A. Subrahmanyam, and Q. Tong. 2014. Have capital market anomalies attenuated in the recent era of high liquidity and trading activity? Journal of Accounting and Economics 58:51–58.
【20】Cochrane, J. H. 2011. Discount rates. Journal of Finance 66:1047–1108.
【21】Cooper, M. J., H. Gulen, and M. J. Schill. 2008. Asset growth and the cross section of asset returns. Journal of Finance 63:1609–165
【22】Daniel, K., and T. Moskowitz. 2016. Momentum crashes. Journal of Financial Economics 122:221–247.
【23】Ehsani S., and J. T. Linnainmaa. 2019. Factor momentum and the momentum factor. Working Paper.
【24】Fama, E. F. 1998. Market efficiency, long-term returns, and behavioral finance. Journal of Financial Economics 49:283–306
【25】Fama, E. F., and K. R. French. 1993. Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33:3–56.
【26】Fama, E. F., and K. R. French. 2008. Dissecting anomalies. Journal of Finance 63:1653–1678
【27】Fama, E. F., and K. R. French. 2015. A five-factor asset pricing model. Journal of Financial Economics 116:1–22.
【28】Fama, E. F., and K. R. French. 2018. Choosing factors. Journal of Financial Economics 128: 234–252.
【29】Fama, E. F., and J. MacBeth. 1973. Risk, return, and equilibrium: Empirical tests. Journal of Political Economy 71:607–636.
【30】Feng, G., S. Giglio, and D. Xiu. 2019. Taming the factor zoo. Forthcoming in Journal of Finance
【31】Feng, G., N. G. Polson, and J. Xu. 2019. Deep learning in asset pricing. Working Paper.
【32】Freyberger, J., A. Neuhierl, and M. Weber. 2018. Dissecting characteristics nonparametrically. Working Paper
【33】Financial Stability Board (FSB). 2017. Artificial intelligence and machine learning in financial services.
【34】Green, J., J. R. M. Hand, and X. F. Zhang. 2017. The characteristics that provide independent information about average U.S. monthly stock returns. Review of Financial Studies 30:4389–4436.
【35】Green, R. C., and B. Hollifield. 1992. When will mean-variance efficient portfolios be well diversified? Journal of Finance 47:1785–1809.
【36】Griffin, J. M., J. H. Harris, T. Shu, and S. Topaloglu. 2011. Who drove and burst the tech bubble? Journal of Finance 66:1251–1290.
【37】Gromb, D., and D. Vayanos. 2002. Equilibrium and welfare in markets with financially constrained arbitrageurs. Journal of Financial Economics 66:361–407.
【38】Gu, S., B. Kelly, and D. Xiu. 2019. Empirical asset pricing via machine learning. Forthcoming in Review of Financial Studies
【39】Hameed, A., and G. M. Mian. 2015. Industries and stock return reversals. Journal of Financial and Quantitative Analysis 50:89–117.
【40】Han, Y., A. He, D. Rapach, and G. Zhou. 2019. Firm characteristics and expected stock returns. Working Paper.
【41】Hansen, L. P., and R. Jagannathan. 1991. Implications of security market data for models of dynamic economies. Journal of Political Economy 99:225–262.
【42】Harvey, C. R., Y. Liu, and H. Zhu. 2016. ...and the cross-section of expected returns. Review of Financial Studies 29:5–68
【43】Heaton, J. B., N. G. Polson, and J. H. Witte. 2017. Deep learning for finance: Deep portfolios. Applied Stochastic Models in Business and Industry 33:3–12
【44】Hong, H., T. Lim, and J. C. Stein. 2000. Bad news travels slowly: Size, analyst coverage, and the profitability of momentum strategies. Journal of Finance 55:265–295
【45】Hou, K., C. Xue, and L. Zhang. 2015. Digesting anomalies: An investment approach. Review of Financial Studies 28:650–705.
【46】Hou, K., C. Xue, and L. Zhang. 2018. Replicating anomalies. Forthcoming in Review of Financial Studies
【47】Jegadeesh, N. 1990. Evidence of predictable behavior of security returns. Journal of Finance 45:881–898.
【48】Jiang, G., C. M. C. Lee, and Y. Zhang. 2005. Information uncertainty and expected returns. Review of Accounting Studies 10:185–221.
【49】Kelly, B., S. Pruitt, and Y. Su. 2018. Characteristics are covariances: A unified model of risk and return. Working Paper.
【50】Kozak, S., S. Nagel, and S. Santosh. 2019. Shrinking the cross-section. Forthcoming in Journal of Financial Economics
【51】Lettau, M., and M. Pelger. 2018a. Estimating latent asset-pricing factors. Forthcoming in Journal of Econometrics.
【52】Lettau, M., and M. Pelger. 2018b. Factors that fit the time series and cross-section of stock returns. Working Paper
【53】Litzenberger, R. H., and K. Ramaswamy. 1982. The effects of dividends on common stock prices: Tax effects or information effects? Journal of Finance 37:429–443.
【54】McLean, R., and J. Pontiff. 2016. Does academic research destroy stock return predictability? Journal of Finance 71:5–31.
【55】Miller, E. M. 1977. Risk, Uncertainty, and divergence of opinion. Journal of Finance 32:1151–1168.
【56】Nagel, S. 2012. Evaporating liquidity. Review of Financial Studies 25:2005–2039
【57】Newey, W. K., and K. D. West. 1987. A simple positive-definite heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica 55:703–708.
【58】Novy-Marx, R. 2013. The other side of value: The gross profitability premium. Journal of Financial Economics 108:1–28
【59】Novy-Marx, R., and M. Velikov. 2016. A taxonomy of anomalies and their trading costs. Review of Financial Studies 29:104–147
【60】Pástor, L., and R. Stambaugh. 2003. Liquidity risk and expected stock returns. Journal of Political Economy 113:642–685.
【61】Pontiff, J., and A. Woodgate. 2008. Share issuance and cross-sectional returns. Journal of Finance 63:921– 945.
【62】Rasekhschaffe, K. C., and R. C. Jones. 2019. Machine learning for stock selection. Financial Analysts Journal 75:70–88
【63】Sloan, R. G. 1996. Do stock prices fully reflect information in accruals and cash flows about future earnings? Accounting Review 71:289–315.
【64】Stambaugh, R. F., J. Yu, and Y. Yuan. 2012. The short of it: Investor sentiment and anomalies. Journal of Financial Economics 104:288–302
【65】Stambaugh, R. F., J. Yu, and Y. Yuan. 2015. Arbitrage asymmetry and the idiosyncratic volatility puzzle. Journal of Finance 70:1903–1948.
【66】Stambaugh, R. F., J. Yu, and Y. Yuan. 2017. Mispricing factors. Review of Financial Studies 30:1270– 1315
【67】Titman, S., K. Wei, and F. Xie. 2004. Capital investments and stock returns. Journal of Financial and Quantitative Analysis 39:677–700
【68】Welch, I., and A. Goyal. 2008. A comprehensive look at the empirical performance of equity premium prediction. Review of Financial Studies 21:1455–1508
注:文中报告节选自兴业证券经济与金融研究院已公开发布研究报告,具体报告内容及相关风险提示等详见完整版报告。
证券研究报告:《机器学习模型的实践探索:在交[文]易限制下能否有效预测股票收益?》
对外发布时间:2023年10月12日
报告发布机构:兴业证券股份有限公司(已获中国[章]证监会许可的证券投资咨询业务资格)
----------------------[来]----------------
分析师:郑兆磊
SAC执业证书编号:S01905200800[自]06
E-mail: [email protected].[1]cn
分析师:占康萍
SAC执业证书编号:S01905220700[7]08
E-mail:zhankangping@xy[量]zq.com.cn
----------------------[化]----------------
更多量化最新资讯和研究成果,欢迎关注我们的微[ ]信公众平台(微信号:XYQuantResea[ ]rch)!
本篇文章来源于微信公众号: XYQuantResearch





